各类激活函数

激活函数

为什么要使用激活函数？

激活函数用来怎加非线性因素的，提高模型拟合能力。如果不存在激活函数，神经网络的每一层的输入都是对前面输入的线性变化，就算把网络加到很深也无法去拟合任意函数的。

激活函数具有的特性

虽然我们常用激活函数不是很多，那是否只有这些函数能作为激活函数呢？我们从神经网络的工作过程中看，激活函数具有什么样的性质能够更好的帮助神经网络的训练。

• 非线性：数，激活函数必须是非线性的。
• 计算简单：神经元都要经过激活运算的，在随着网络结构越来越庞大、参数量越来越多，激活函数如果计算量小就节约了大量的资源。
• f ( x ) ≈ x:在向前传播时，如果参数的初始化是随机量的最小值，神经网络的训练很高效。在训练的时候不会出现输出的幅度随着不断训练发生倍数的增长，是网络更加的稳定，同时也使得梯度更容易回传。
• 可微：因为神经网络要通过反向传播来跟新参数，如果激活函数不可微，就无法根据损失函数对权重求偏导，也就无法更新权重。传统的激活函数如sigmoid等满足处处可微。对于分段线性函数比如ReLU，只满足几乎处处可微（即仅在有限个点处不可微）。对于SGD算法来说，由于几乎不可能收敛到梯度接近零的位置，有限的不可微点对于优化结果不会有很大影响。
• 非饱和性：（饱和函数有Sigmoid、Tanh等，非饱和函数ReLU等）例如Sigmoid函数求导以后的值很小，两端的值接近为零在反向传播的时候，如果网络的层次过大便会发生梯度消失的问题，使得浅层的参数无法更新。（梯度消失后面会介绍）
• 单调性：当激活函数单调时，单层网络保证是凸函数。
• 输出值的范围： 当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的Learning Rate。

sigmoid

sigmoid函数，也就是s型曲线函数，如下：

原函数图像：

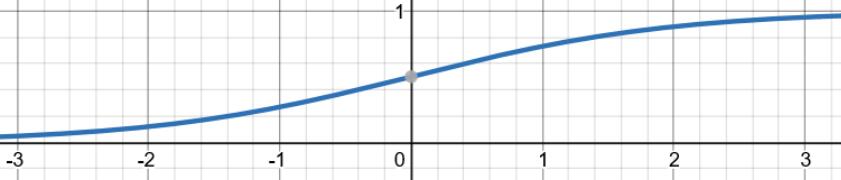
函数性质

• 非线性函数
• 求导简单，函数求导后为f′(x)=f(x)(1−f(x))
• 不满足f ( x ) ≈ x
• 在定义域内处处可导
• 饱和激活函数
• 函数为单调函数
• 函数的输出区间在（0，1）之间，函数定义域为负无穷到正无穷

倒数及其导数图像：

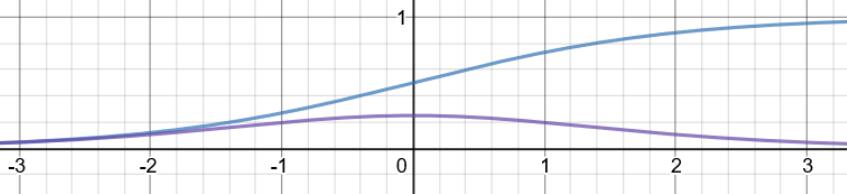
优点和缺点

• 优点：平滑、容易求导
• 缺点：
  • 激活函数运算量大（包含幂的运算）
  • 函数输出不关于原点对称，使得权重更新效率变低，同时这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入，随着网络的加深，会改变数据的原始分布
  • 由图像知道导数的取值范围[0,0.25]，非常的小。在进行反向传播计算的时候就会乘上一个很小的值，如果网络层次过深，就会发生“梯度消失”的现象了，无法更新浅层网络的参数了。

hard sigmoid

函数公式：

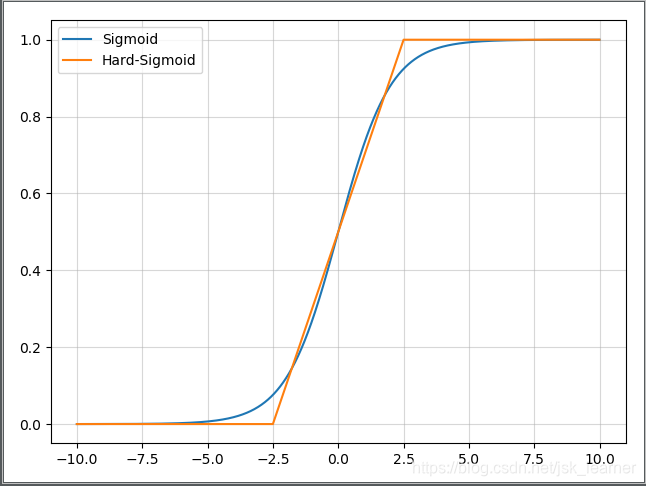
解释：当 x < -2.5输出0，当 x > 2.5时，输出1，当 -2.5 < x & x < 2.5时，输出为 (2x+5) / 10，线性函数。
那么其导数，当 x < -2.5输出0，当 x > 2.5时，输出0，当 -2.5 < x & x < 2.5时，输出为 1 / 5。

hard-Sigmoid函数时Sigmoid激活函数的分段线性近似。从公示和曲线上来看，其更易计算，因此会提高训练的效率，不过同时会导致一个问题：就是首次派生值为零可能会导致神经元died或者过慢的学习率。

函数图像：

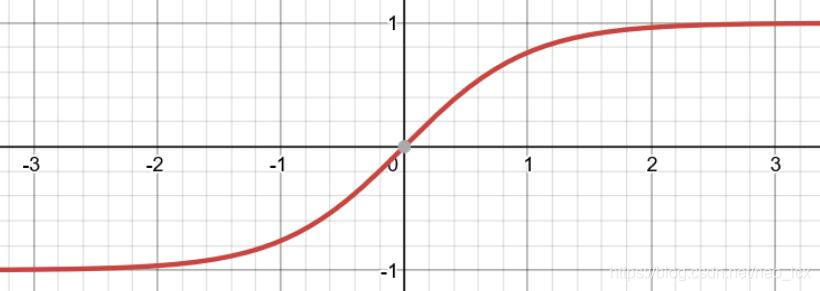
Tanh(双曲正切函数)激活函数

函数图像：

函数公式：

$$f\left( x\right) =\dfrac{\left( e^{x}-e^{-x}\right) }{\left( e^{x}+e^{-x}\right) }$$

导数公式:

$$f\left( x\right) =1-\left( f\left( x\right) \right) ^{2}$$

倒数图像：

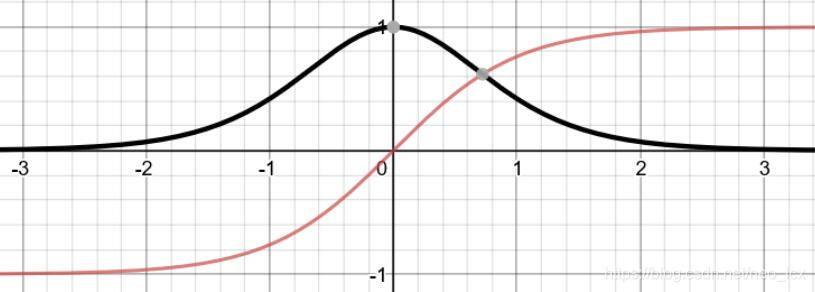
函数性质

• 非线性函数
• 求导简单
• 不满足f ( x ) ≈ x
• 饱和激活函数
• 函数为单调函数
• 函数的输出区间在（-1，1）之间，函数定义域为负无穷到正无穷

优点与缺点：

• 优点：
  • 解决了Sigmoid的输出不关于零点对称的问题
  • 也具有Sigmoid的优点平滑，容易求导
• 缺点：
  • 激活函数运算量大（包含幂的运算）
  • Tanh的导数图像虽然最大之变大，使得梯度消失的问题得到一定的缓解，但是不能根本解决这个问题

ReLU激活函数

ReLU函数代表的的是“修正线性单元”，它是带有卷积图像的输入x的最大函数(x,o)。ReLU函数将矩阵x内所有负值都设为零，其余的值不变

函数公式：

$$f\left( x\right) =\max \left( 0,x\right)$$

函数图像：

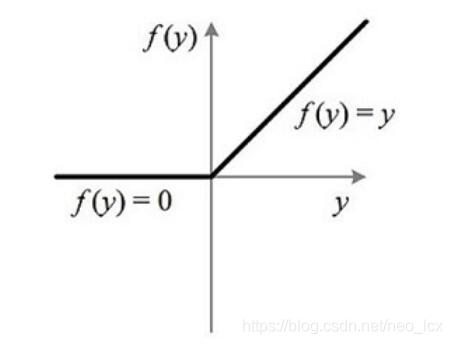
激活函数的性质：

• 非线性函数（虽然单侧是线性函数）
• 计算简单是真的简单(不管是在神经网络向前计算过程中还是反向传播的时候)
• 右侧满足f ( x ) ≈ x {\rm{f}}(x) \approx xf(x)≈x
• 右侧为单调函数
• 输出为（0，+无穷）

优点和缺点：

• 优点

  • 计算量小，相对于之前使用sigmoid和Tanh激活函数需要进行指数运算，使用ReLu的计算量小很多，在使用反向传播计算的时候也要收敛更更快。

  • 缓解了在深层网络中使用sigmoid和Tanh激活函数造成了梯度消失的现象（右侧导数恒为1）

  • 缓解过拟合的问题。由于函数的会使小于零的值变成零，使得一部分神经元的输出为0，造成网络的稀疏

    性，减少参数相互依赖的关系缓解过拟合的问题（请问人工神经网络中的activation function的作用具体是什么？为什么ReLu要好过于tanh和sigmoid function?）

• 缺点

  • 造成神经元的“死亡”（详细的介绍见连接深度学习中，使用relu存在梯度过大导致神经元“死亡”，怎么理解？）

  解决方法：优化函数，采用较小学习速率，采用momentum based 优化算法

  • ReLU的输出不是0均值的

Leaky ReLU 变种激活函数

函数公式：

f ( x ) = max ⁡ ( α x , x )

函数图像：

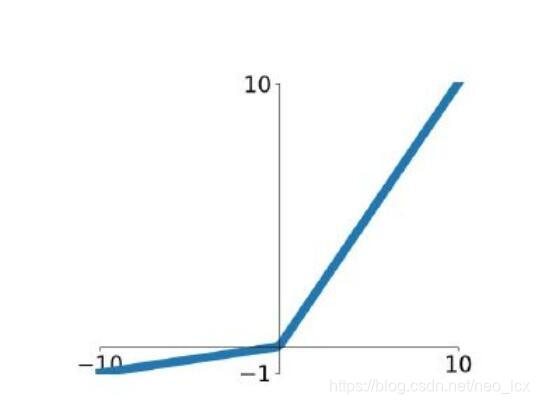
函数图像跟之前的ReLu图像很像，同样的PReLU和ELU激活函数也是在ReLu的基础上针对ReLU在训练时神经元容易死亡做出了优化，基本的思路就是让函数小于0的部分不直接为0，而是等于一个很小的数，使得负轴的信息不至于完全丢弃。

softmax

softmax函数，又称**归一化指数函数。**它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。

下面为大家解释一下为什么softmax是这种形式。

首先，我们知道概率有两个性质：1）预测的概率为非负数；2）各种预测结果概率之和等于1。

softmax就是将在负无穷到正无穷上的预测结果按照这两步转换为概率的。

1）将预测结果转化为非负数

下图为y=exp(x）的图像，我们可以知道指数函数的值域取值范围是零到正无穷。softmax第一步就是将模型的预测结果转化到指数函数上，这样保证了概率的非负性。

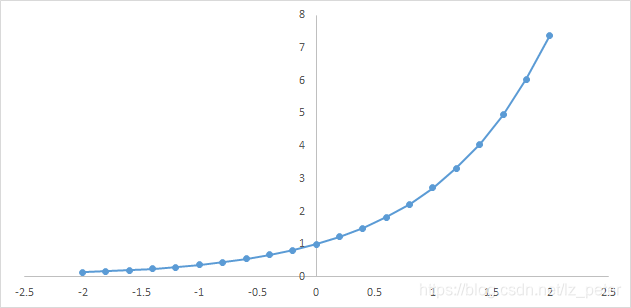
2）各种预测结果概率之和等于1

为了确保各个预测结果的概率之和等于1。我们只需要将转换后的结果进行归一化处理。方法就是将转化后的结果除以所有转化后结果之和，可以理解为转化后结果占总数的百分比。这样就得到近似的概率。

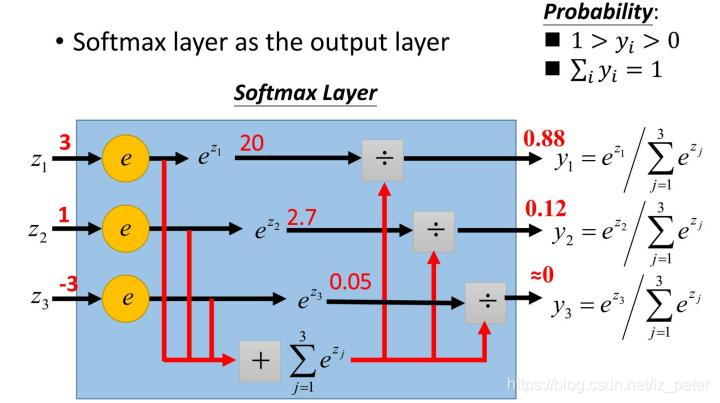
下面为大家举一个例子，假如模型对一个三分类问题的预测结果为-3、1.5、2.7。我们要用softmax将模型结果转为概率。步骤如下：

1）将预测结果转化为非负数

y1 = exp(x1) = exp(-3) = 0.05

y2 = exp(x2) = exp(1.5) = 4.48

y3 = exp(x3) = exp(2.7) = 14.88

2）各种预测结果概率之和等于1

z1 = y1/(y1+y2+y3) = 0.05/(0.05+4.48+14.88) = 0.0026

z2 = y2/(y1+y2+y3) = 4.48/(0.05+4.48+14.88) = 0.2308

z3 = y3/(y1+y2+y3) = 14.88/(0.05+4.48+14.88) = 0.7666

总结一下softmax如何将多分类输出转换为概率，可以分为两步：

1）分子：通过指数函数，将实数输出映射到零到正无穷。

2）分母：将所有结果相加，进行归一化。

SELU（可伸缩的指数线性单元）

SELU Scaled Exponential Linear Unit等同于：scale * elu(x, alpha)，其中 alpha 和 scale 是预定义的常量。只要正确初始化权重（参见 lecun_normal 初始化方法）并且输入的数量「足够大」（参见参考文献获得更多信息），选择合适的 alpha 和 scale 的值，就可以在两个连续层之间保留输入的均值和方差。

函数形式：

深度学习在卷积神经网络和循环神经网络取得很大突破，但标准前馈网络的成功消息却很少。因此引入自归一化的神经网络，来尝试进行高级抽象表示。
这种自归一化的神经网络的激活函数就是selu，它也是一种基于激活函数的正则化方案。它具有自归一化特点，即使加入噪声也能收敛到均值为0、方差为1或方差具有上下界。
优点：在全连接层效果好，可以避免梯度消失和爆炸。
缺点：在卷积网络效果尚未证明。可能引起过拟合。

ELU（指数线性单元）

其将激活函数的平均值接近零，从而加快学习的速度。同时，还可以通过正值的标识来避免梯度消失的问题。根据一些研究，ELU的分类 精确度要高于Relu。

函数公式：

函数图像：

• 融合了sigmoid和ReLU，左侧具有软饱和性，右侧无饱和性。
• 右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱能够让ELU对输入变化或噪声更鲁棒。
• ELU的输出均值接近于零，所以收敛速度更快。
• 在 ImageNet上，不加 Batch Normalization 30 层以上的 ReLU
  网络会无法收敛，PReLU网络在MSRA的Fan-in （caffe ）初始化下会发散，而 ELU
  网络在Fan-in/Fan-out下都能收敛。

SELU（给ELU乘个系数）

函数公式：

函数图像：

lambda为系数

P-Relu（参数化修正线性单元）

可以看作是Leaky ReLU的一个变体，不同的是，P-ReLU中的负值部分的斜率是根据数据来定的，即a的值并不是一个常数。

R-Relu（随机纠正线性单元）

R-ReLU也是Leaky ReLU的一个变体，只不过在这里负值部分的斜率在训练的时候是随机的，即在一个范围内随机抽取a的值，不过这个值在测试环节会固定下来。

Swish

函数公式：

导数公式：

函数图像：

导数图像：

当β = 0时,Swish变为线性函数f(x)=x2f(x)=x2.
β → ∞, σ(x)=(1+exp(−x))−1σ(x)=(1+exp⁡(−x))−1为0或1. Swish变为ReLU: f(x)=2max(0,x)
所以Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数.

Mish

函数公式

公式推导：

Mish和Swish中参数=1的曲线对比：（第一张是原始函数，第二张是导数）

优点

以上无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许允许更好的梯度流，而不是像ReLU中那样的硬零边界。

最后，可能也是最重要的，目前的想法是，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。

要区别可能是Mish函数在曲线上几乎所有点上的平滑度

Maxout

与常规的激活函数不同，Maxout是一个可以学习的分段线性函数。
其可以看做是在深度学习网络中加入了一层激活函数层，包含一个参数k，这一层相比ReLU，Sigmoid等，其在于增加了k个神经元，然后输出激活值最大的值。
其需要学习的参数就是k个神经元中的权值和偏置，这就相当于常规的激活函数一层，而Maxout是两层，而且参数个数增加了K倍。
其可以有效的原理是，任何ReLU及其变体等激活函数都可以看成分段的线性函数，而Maxout加入的一层神经元正是一个可以学习参数的分段线性函数。

优点：其拟合能力很强，理论上可以拟合任意的凸函数；
具有ReLU的所有优点，线性和非饱和性；
同时没有ReLU的一些缺点，如神经元的死亡；
缺点：导致整体参数的激增。

网络图片：

关于激活函数统一说明

ELU在正半轴取输入x奸情了梯度弥散情况（正半轴导数处处为1），而这一点特性，基本上除了swish其他非饱和激活函数都具有这个特性。而只有ReLU在负半轴的输出没有复制，所以ReLU的输出均值一定是大于0的，而当激活值的均值非0时，会对下一层造成以bias，也就是下一层的激活单元会出现bias shift现象，通过不断的层数叠加，bias shift会变得非常大。而ELU可以让激活函数的输出均值尽可能接近0，类似于BN操作，但是计算复杂度更低。而且虽然Leaky ReLU和PReLU等都有负值，但是它们不保证在不激活的状态对噪声鲁棒，这里的不激活指的是负半轴。而ELU在输入取较小值时具有软饱和的特性，提升了对噪声的鲁棒性。Swish和ELU都是可以取负值，同时在负半轴具有软饱和的性能，提高了对噪声的鲁棒性，SELU效果比ELU效果还要更好。