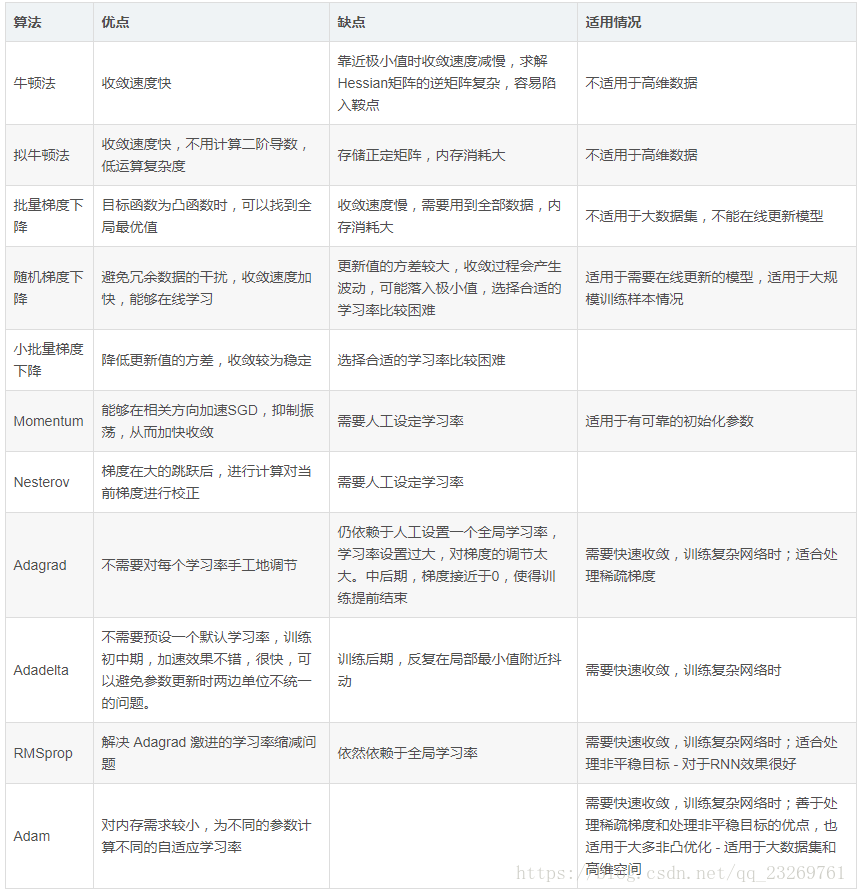
优化算法
SGD、BGD、MBGD
现在所说的SGD一般都指MBGD(小批量梯度下降法Mini-batch Gradient Descent)。
三种梯度下降的方法用于更新参数,也就是当前参数等于上一时刻参数减去学习率乘以梯度。
 三种方法的不同体现在计算梯度上
假设损失函数为二次函数,那么参数θ的更新公式为
三种方法的不同体现在计算梯度上
假设损失函数为二次函数,那么参数θ的更新公式为

SGD(随机梯度下降法Stochastic Gradient Descent)
SGD:mini-batch gradient descent(随机梯度下降)
SGD就是每一次迭代每次只用一个样本计算mini-batch的梯度,然后对参数进行更新,是最常见的优化方法了。
<img src=“https://ftp.bmp.ovh/imgs/2021/07/742b1819c08ba909.png” style=“zoom: 67%;” /
优点是速度快,缺点是可能陷入局部最优,搜索起来比较盲目,并不是每次都朝着最优的方向(因为单个样本可能噪音比较多),走的路径比较曲折(震荡)。


BGD (批梯度下降算法 Batch Gradient Descent)
计算梯度时候使用所有的数据来计算,取平均值(最原始的梯度下降算法)。
BGD算法,每走一步(更新模型参数),为了计算original-loss上的梯度,就需要遍历整个数据集,在一般深度学习任务中,这是很不现实的。
好处在于收敛次数少,坏处就是每次迭代需要用到所有数据,占用内存大耗时大。

MBGD (小批量梯度下降法Mini-batch Gradient Descent)
SGD和BGD是两个极端, 而MBGD是两种方法的折中,每次选择一批数据(不是全部,也不是单个)来求梯度。
该方法也容易陷入局部最优。
现在所说的SGD基本都是MBGD。
其中是模型参数,
是模型目标函数,
是目标函数的梯度,
是学习率。
SGD完全依赖于当前batch的梯度,所以η可理解为允许当前batch的梯度多大程度影响参数更新。
缺点:(正因为有这些缺点才让这么多大神发展出了后续的各种算法)
- 选择合适的learning rate比较困难。
- 对所有的参数更新使用同样的learning rate。对于稀疏数据或者特征,有时我们可能想更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些,这时候SGD就不太能满足要求了。
- SGD容易收敛到局部最优,在某些情况下可能被困在鞍点。【但是在合适的初始化和学习率设置下,鞍点的影响其实没这么大】
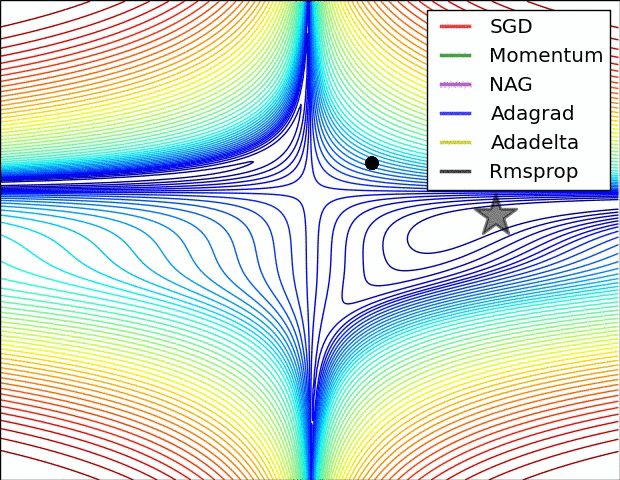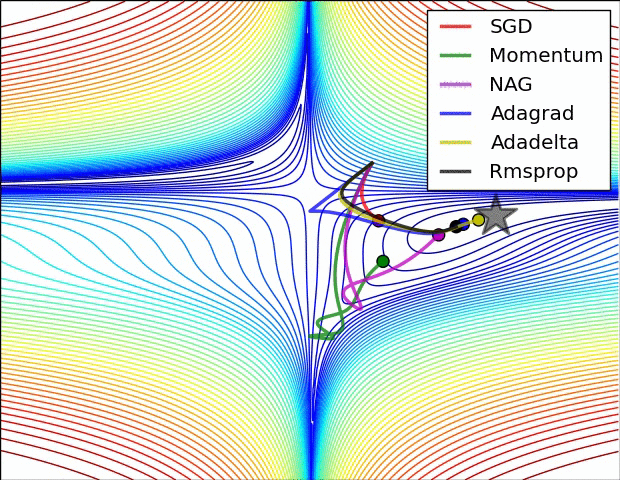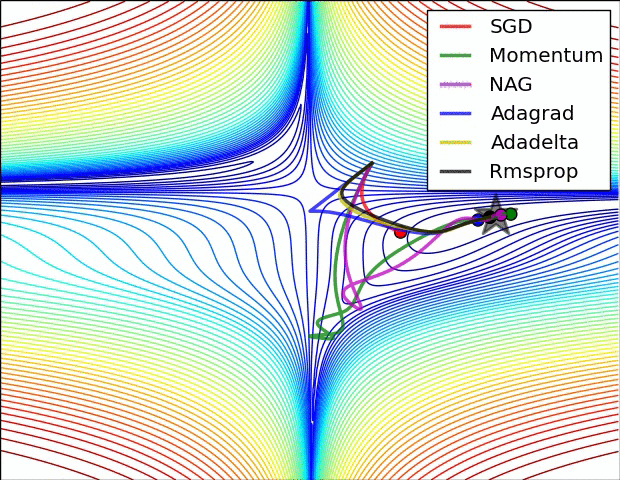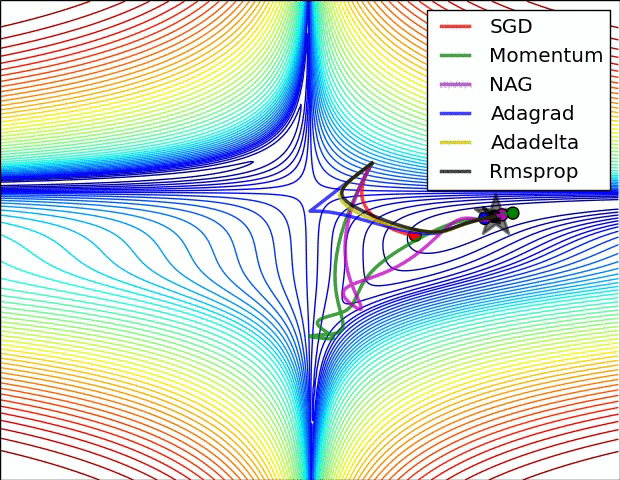
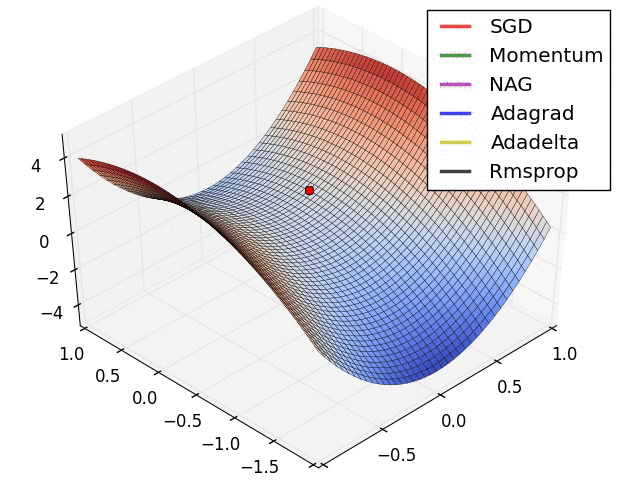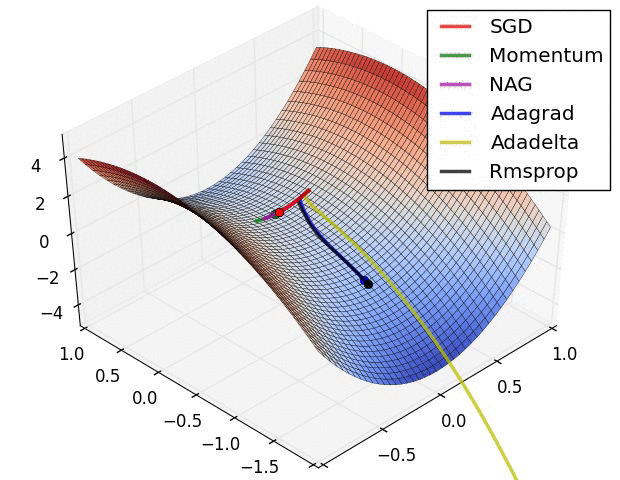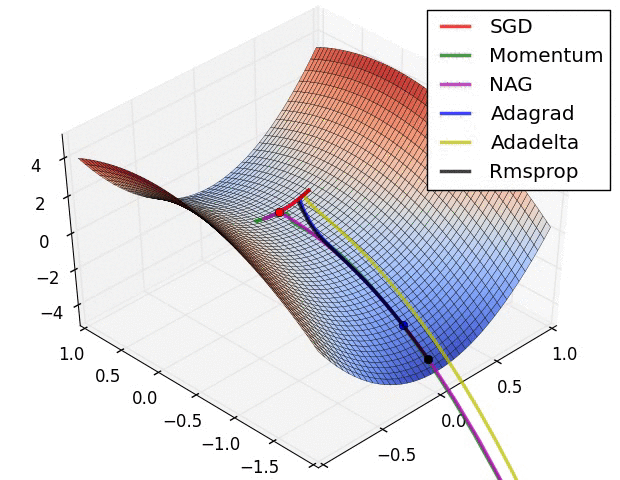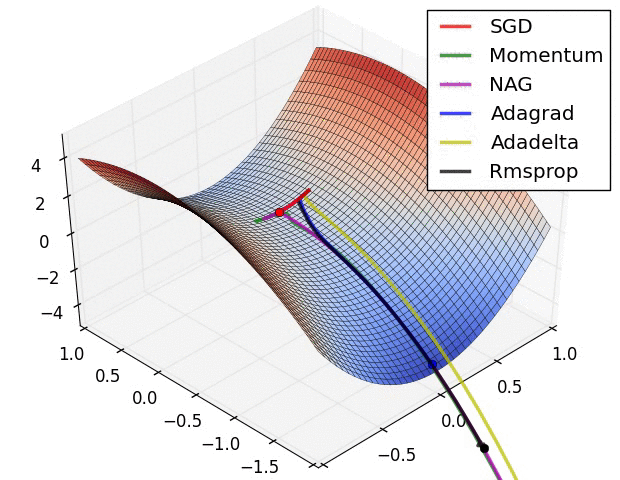
- “之字形”的出现,即在陡谷(一种在一个方向的弯曲程度远大于其他方向的表面弯曲情况)处震荡。如下图所示
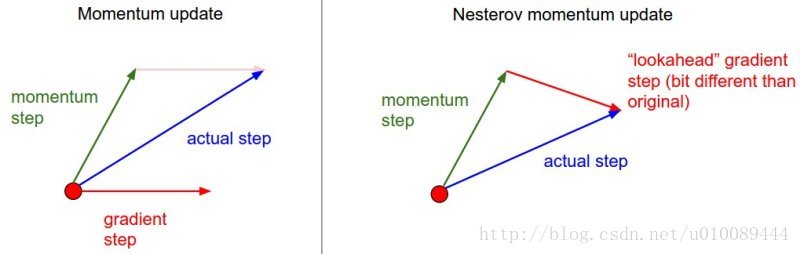
NAG(牛顿动量 Nesterov accelerated gradient)
1 | 1.Nesterov是Momentum的变种。 |
在小球向下滚动的过程中,我们希望小球能够提前知道在哪些地方坡面会上升,这样在遇到上升坡面之前,小球就开始减速。这方法就是Nesterov Momentum,其在凸优化中有较强的理论保证收敛。并且,在实践中Nesterov Momentum也比单纯的 Momentum 的效果好:

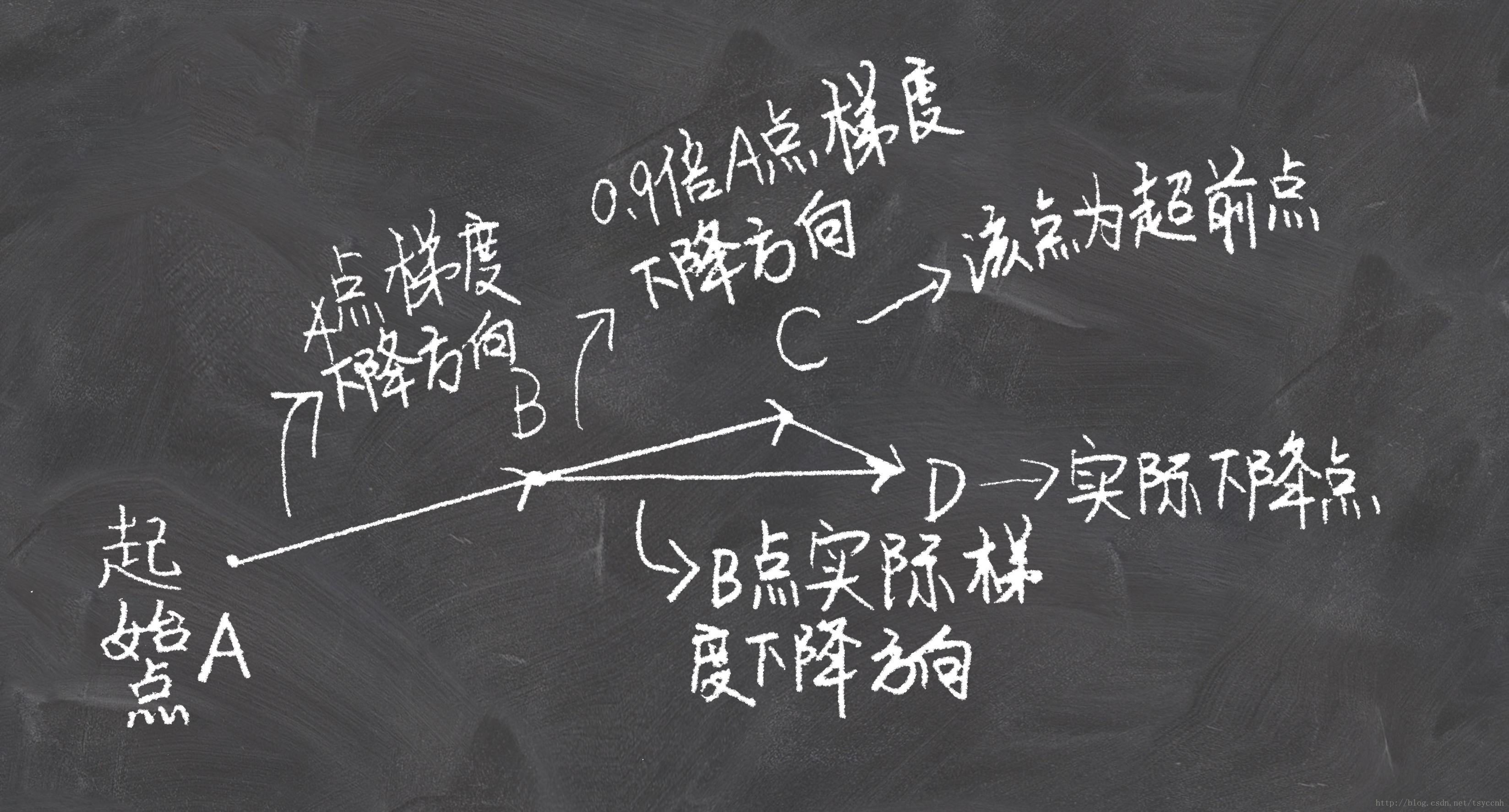
其核心思想是:注意到 momentum 方法,如果只看 γ * v 项,那么当前的 θ经过 momentum 的作用会变成 θ-γ * v。因此可以把 θ-γ * v这个位置看做是当前优化的一个”展望”位置。所以,可以在 θ-γ * v求导, 而不是原始的θ。
我们使用来移动,通过计算
,我们能够得到一个下次参数位置的近似值——也就是能告诉我们参数大致会变为多少。那么,通过基于未来参数的近似值(站的更远看看)而非当前的参数值计算相得应罚函数
并求偏导数,我们能让优化器高效地「前进」并收敛:

优点:
这种基于预测的更新方法,使我们避免过快地前进,并提高了算法地响应能力,大大改进了 RNN 在一些任务上的表现【为什么对RNN好呢,不懂啊】
没有对比就没有伤害,NAG方法收敛速度明显加快。波动也小了很多。实际上NAG方法用到了二阶信息,所以才会有这么好的结果。先按照原来的梯度走一步的时候已经求了一次梯度,后面再修正的时候又求了一次梯度,所以是二阶信息。
AdaGrad
AdaGrad 算法根据自变量在每个维度的梯度值调整各个维度的学习率,从而避免统一的维度难以适应所有维度的问题。
adagrad 方法是将每一个参数的每一次迭代的梯度取平方累加再开方,用基础学习率除以这个数,来做学习率的动态更新。【这样每一个参数的学习率就与他们的梯度有关系了,那么每一个参数的学习率就不一样了!也就是所谓的自适应学习率】。
Adagrad其实是对学习率进行了一个约束。即:
此处,对从1到
进行一个递推形成一个约束项regularizer,
,
用来保证分母非0

特点:
- 前期
较小的时候, regularizer较大,能够放大梯度
- 后期
较大的时候,regularizer较小,能够约束梯度
- 适合处理稀疏梯度
缺点:
- 由公式可以看出,仍依赖于人工设置一个全局学习率
设置过大的话,会使regularizer过于敏感,对梯度的调节太大
- 中后期,分母上梯度平方的累加将会越来越大,使
,使得训练提前结束
Adadelta
Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项【其实就是相当于指数滑动平均,只用了前多少步的梯度平方平均值】,并且也不直接存储这些项,仅仅是近似计算对应的平均值【这也就是指数滑动平均的优点】
RMSprop依然需要自己设定全局学习率,因此Adadelta在RMSprop的基础上,用参数更新的平方来替代全局学习率的位置,这样就可以省略全局学习率了。
特点:
- 训练初中期,加速效果不错,很快
- 训练后期,反复在局部最小值附近抖动
momentum(动量梯度下降 Gradient Descent With Momentum)


RMSProp


由于AdaGrad单调递减的学习率变化过于激进,RMSprop只关注过去一段时间的梯度平均值,离的时间越远越不重要。
特点:
- 其实RMSprop依然依赖于全局学习率
- RMSprop算是Adagrad的一种发展,和Adadelta的变体,效果趋于二者之间
- 适合处理非平稳目标(也就是与时间有关的)
- 对于RNN效果很好,因为RMSprop的更新只依赖于上一时刻的更新,所以适合。???
Adam(Adaptive Moment Estimation)
Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop,它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。公式如下:
其中,,
分别是对梯度的一阶矩估计和二阶矩估计,可以看作对期望
,
的估计;
,
是对
,
的校正,这样可以近似为对期望的无偏估计。 可以看出,直接对梯度的矩估计对内存没有额外的要求,而且可以根据梯度进行动态调整,而
对学习率形成一个动态约束,而且有明确的范围。

特点:
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 对内存需求较小
- 为不同的参数计算不同的自适应学习率
- 也适用于大多非凸优化 - 适用于大数据集和高维空间
Adamax
Adamax是Adam的一种变体,此方法对学习率的上限提供了一个更简单的范围。公式上的变化如下:
可以看出,Adamax学习率的边界范围更简单
Nadam
Nadam类似于带有Nesterov动量项的Adam。公式如下:
可以看出,Nadam对学习率有了更强的约束,同时对梯度的更新也有更直接的影响。一般而言,在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果。