博弈论
博弈论
博弈模型/博弈论/对策论
百科定义
博弈论(英语:Game Theory),又译为对策论或赛局理论,是经济学的一个分支,1944年冯·诺伊曼与奥斯卡·摩根斯特恩合著《博弈论与经济行为》,标志着现代系统博弈理论的的初步形成,因此他们被称为“博弈论之父”。博弈论被认为是20世纪经济学最伟大的成果之一。目前可以应用在生物学、经济学、国际关系、计算机科学、政治学、军事战略,研究游戏或者博弈内的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法。也是运筹学的一个重要学科。 现代的博弈论的源头是约翰·冯·诺伊曼对于双人零和博弈的混合策略均衡点的发想和证明。
模型背景
- 多个决策者
- 每个决策都有自己的决策变量和目标函数
- 一个决策者的决策变量以某种形式出现在另一个决策者的目标函数中
- 决策者之间的决策行为相互影响
具体分类
- 合作博弈:是否达成有约束性的协议
- 静态动态博弈
- 完全信息不完全信息博弈
- 非合作博弈
模型三要素
- 参与人:决策者
- 策略空间:决策变量的取值范围
- 效用函数:决策者的目标函数
学术词汇
- 零和博弈:双方,一方所得即一方所失。
- 策略式博弈(静态博弈)
- 所有玩家同时做策略选择
- 知道对手可选的策略
- 不知道对手具体会选哪一个策略
- 非合作
- 完全信息:所有玩家都知道在一组策略选择下的每个人的收益。
建议看《数学模型》例子很多很详细。
博弈论导论
一、什么是博弈论?
博弈论(Game Theory)是相互依存情况中的理性行为的数学建模。博弈由这几个要素构成:
- 玩家(Players):博弈的参与者
- 策略(Strategy):博弈玩家各自的操作
- 收益(Payoff):博弈玩家的收益,一般用矩阵来表示,在连续的时候也会写成函数。
- 信息(Information):博弈玩家知道的信息
- 理性(Rationality):博弈玩家是理性的,在竞争的情况下使自己的收益最大化
博弈论方法的本质——相互依存性:每一方的收益不仅依赖于自己的策略,同时也依赖其他参与方的策略。
博弈论研究的目标——均衡:因为博弈的参与方的策略改变会造成收益的变化,所以,各玩家会调整策略使自己的收益最大。在这样的情况下,一个“稳定”的策略选择是值得研究的。各个玩家选择了各自的策略之后,没有动机去改变当前的策略,就形成了稳定的状态。
定义是抽象的,还是用一些例子来找找感觉吧。
二、例子:囚徒困境
这个例子应该是众所周知。简要介绍一下:
两个共谋犯罪的人被关入监狱,不能互相沟通情况。①如果两个人都不揭发对方,则由于证据不确定,每个人都坐牢一年;②若一人揭发,而另一人沉默,则揭发者因为立功而立即获释,沉默者因不合作而入狱十二年;③若互相揭发,则因证据确凿,二者都判刑六年。
考察博弈的几个要素:
- 玩家:这两个犯罪的人,记为A、B
- 策略:二者的策略都是{揭发、沉默}
- 收益:用收益矩阵来表示
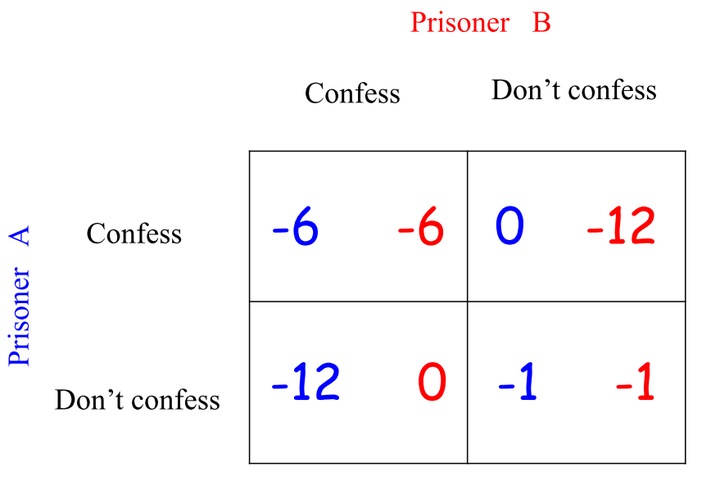 囚徒困境收益矩阵
囚徒困境收益矩阵
\4. 信息:这种情况是完全信息的,即,每一参与者都拥有所有其他参与者的收益函数的准确信息。
剧透一下,囚徒困境的”均衡“,是二人都选择揭发的策略。
三、分类
- 根据玩家数量分为:1人,2人,多人博弈
- 根据“同时做决策”还是“轮流做决策”分为:策略式博弈(静态博弈)和扩展式博弈(动态博弈)、
- 根据信息的了解情况分为:完全信息博弈和非完全信息博弈
- 根据收益分为:零和博弈、非零和博弈
- 合作、非合作博弈
- 根据策略的数量分为:有限博弈和无限博弈
当然,上面的分类很杂,我们的课程主要讲了这几种:
- 完全信息策略式博弈
- 非完全信息策略式博弈
- 完全信息扩展式博弈
- 非完全信息扩展式博弈
- 重复博弈
四、小结
博弈论很有趣的,你会发现很多意想不到的结果。不过,由于博弈论假设每个玩家都是“理性”的,而现实生活却不一定是这样,因此,很多情况下博弈论给出的结论只是一个理论上的参考。
有一些有意思的小例子,算是智力小测试了,感兴趣可以看看:
- Nim博弈:有一堆硬币,总个数是N;有2个玩家,轮流取硬币。每次可以选择取1枚或2枚。取到最后一枚硬币的人获胜。请问先手有必胜策略还是后手?(和N有关)
- 海盗博弈:这个更有意思一些
- 有五个理性的海盗,P1、 P2、 P3 、P4 和P5,找到了100个金币,需要想办法分配金币。海盗们有严格的等级制度:P1 < P2 < P3 < P4 < P5。
- 海盗世界的分配原则是:等级最高的海盗提出一种分配方案。所有的海盗投票决定是否接受分配,包括提议人。并且在票数相同的情况下,提议人有决定权。如果提议通过,那么海盗们按照提议分配金币。如果没有通过,那么提议人将被扔出船外,然后由下一个最高职位的海盗提出新的分配方案。
- 请问,最终每个人分别会获得多少金币呢?
博弈论笔记一:策略式博弈及其纳什均衡
序言中介绍了博弈的要素和博弈的分类,那么,怎么“论”呢?当下最重要的,是将博弈用数学语言来描述出来,也就是形式化。
博弈不同的分类:{策略式,扩展式},{完全信息,非完全信息}等等,都有不同的形式化表示,这一节介绍最简单的一种:完全信息策略式博弈。
与之对应的例子有:囚徒困境(Prisoners’ Dilemma)、古诺竞争(Cournot Competition)。
对了,顺便提一下,博弈不是“搏”而是“博”,哈哈,一开始学的时候写错了。
一、一些概念的定义
1. 策略式博弈
策略式博弈也叫静态博弈,它是一次博弈:
- 所有玩家同时做策略选择
- 知道对手可选的策略
- 不知道对手具体会选哪一个策略
- 非合作
典型的例子是:石头剪刀布。
与策略式博弈相对应的是扩展式博弈(动态博弈)。
2. 完全信息
所有玩家都知道在一组策略选择下的每个人的收益。
下面把完全信息策略式博弈简写为:策略式博弈
二、策略式博弈形式化
形式化主要是将博弈的要素用数学语言表示出来。对于一个策略式博弈,用{玩家、策略、收益}就可以完全表示。
1. 基础概念的定义
一个策略式博弈包括:
- 玩家集N:玩家的有限集合
- 每个玩家
都有策略集
,表示他可以选择的策略的集合
- 每个玩家
都有收益函数
:
,表示在一组策略下它的收益
此外,有如下定义:
- 博弈结果:
,是一组策略构成的元组
- 博弈结果空间:
,则
- 对手策略:
,则
在策略式博弈中,收益的具体数值并不重要,重要的是收益之间的大小关系,称作偏好关系。任何满足全序关系的集合,都可以用来表示收益。我们通常用实数来表示收益。
2. 形式化
集合 称作策略式博弈G
其中就是前面定义的那样。
3. 例子:囚徒困境形式化
- 玩家集:
,表示1、2两个囚徒
- 策略集:
,为了书写简便,用c表示坦白,用d表示沉默
- 收益函数:
- 用收益矩阵表示如下:
 囚徒困境收益矩阵
囚徒困境收益矩阵
三、纳什均衡
我们自然地会去想,在这种条件下,两个囚犯会选择怎样的策略呢?先从A的视角想一下,
- 如果B坦白:A选择坦白,收益是(-6);A选择沉默,收益是(-12),因此A会坦白。
- 如果B沉默:A选择坦白,收益是(0);A选择沉默,收益是(-1),因此A会坦白。
同理,B也是这么想的,因此,两人都会选择坦白。
1. 纳什均衡的想法
从上面的思考中,可以看出这种思想:当对手策略选定的时候,我会调整自己的策略,使得自己收益在几种策略选择中是最大的,这时的策略称为“最优反应”。这个时候,如果对手不改变策略的话,我是没有动机去改变自己的策略的。
如果每个人的策略都是“最优反应”,那么就会形成一种稳定的局面,这时的博弈结果就是纳什均衡
2. 纳什均衡形式化定义
纳什均衡(Nash equilibrium)是博弈结果,使得对于每个玩家
都有:
(对手策略选定的时候,自己最优)
纳什均衡简写为:NE
3. 纳什均衡求解:寻找最优反应
玩家关于对手策略
的最优反应:
同时满足所有人的最优反应的博弈结果,就是纳什均衡。也就是对于 ,满足
的博弈结果。
4. 例1:依旧是囚徒困境

在收益矩阵上标出这些最优反应:
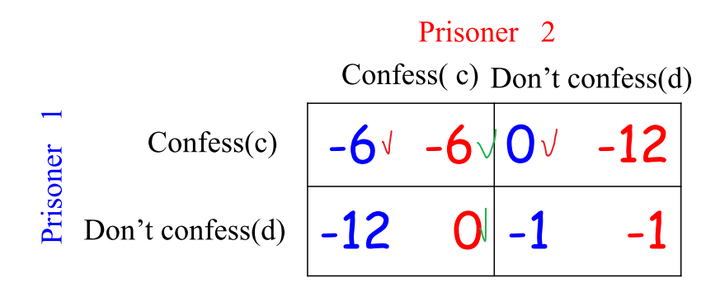
表示在囚徒2选择c的时候,囚徒1会选择c,因为囚徒1的收益(-6 > -12)。对应矩阵中左边红色的”√“。
详细分析如下:
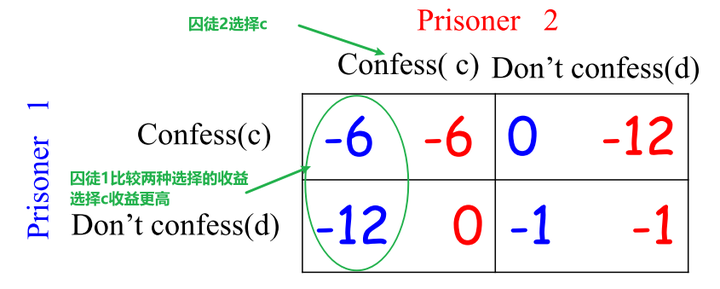
表示在囚徒2选择d的时候,囚徒1会选择c,因为囚徒1的收益(0 > -1)。对应矩阵中右边红色的”√“。
表示在囚徒1选择c的时候,囚徒2会选择c,因为囚徒2的收益(-6 > -12)。对应矩阵中上边绿色的”√“。
表示在囚徒1选择d的时候,囚徒2会选择c,因为囚徒2的收益(0 > -1)。对应矩阵中下边绿色的”√“。
因此,最终得到满足所有人最优反应的结果:(c,c),也就是两人都坦白。
5. 例2:古诺竞争
这个例子收益是连续的,不能用矩阵来表示。问题如下:
两个厂商{1, 2}生产和销售同一种商品,厂商
生产的数量记为
。 每件商品生产成本都是c,售价是:
求纳什均衡
1) 形式化
其中,收益。(售价-成本)x生产数量
2) 求最优反应函数
对于厂商1:
- 如果
,那么对于任意的
,都有
,即没有正收益
- 如果
,那么
。
- 固定
,
何时取最大呢?求导!
- 求解:
,求得
,这就是厂商1的最优反应函数
同理,对于厂商2,最优反应函数是:
3) 纳什均衡
对于满足纳什均衡的博弈结果,有:
联立方程,解得
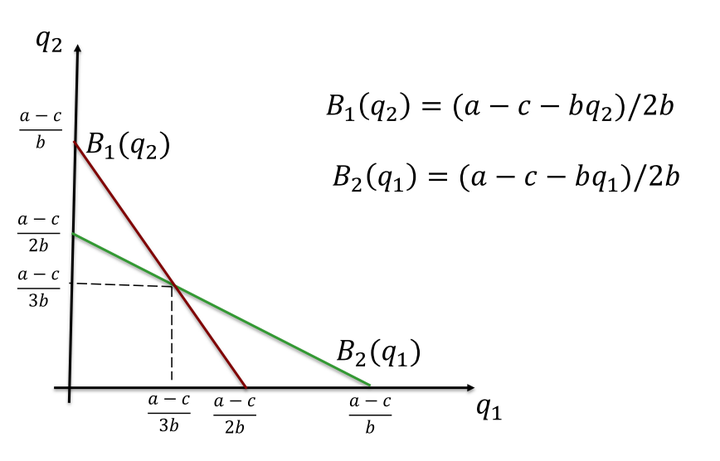 最优反应相交之处
最优反应相交之处
四、小结
这节学习了:
- 策略式博弈形式化
- 纳什均衡的定义及求解
重要的是理解纳什均衡所表示的意义。纳什均衡并不一定是最优的结果,它是一种稳定的局面,在这种情况下,所有人都没有动机去改变自己的选择。
博弈论笔记二:混合策略博弈
一、引言
前面,我们学习了策略式博弈的纳什均衡。每个玩家可选的策略也叫纯策略。在前面讲的纳什均衡中,每个玩家都要选定一个纯策略。但有的时候并不能找到一个纯策略的纳什均衡,举例如下:
 没有纯策略纳什均衡
没有纯策略纳什均衡
还有一个常见的例子:石头剪刀布,就没有纯策略的纳什均衡。
这个时候,需要引入新的概念——混合策略。
二、混合策略博弈
以石头剪刀布为例,无论双方采用哪种策略组合,输的一方总可以改变策略使自己反败为胜,因此没有纯策略的纳什均衡。通过引入“随机性”来解决这个问题。
通俗地解释,混合策略就是在纯策略上加上概率,在一次博弈中,玩家随机地选择一种纯策略。
1. 混合策略
1)纯策略
在前面的一节学习了纯策略的表示:玩家i的策略集,纯策略
。
2)混合策略
混合策略是给每个纯策略分配一个概率,一个玩家的策略集就是一个“样本空间”。
用表示
上的概率分布,即:
那么,混合策略
3)混合策略博弈结果
混合策略博弈的博弈结果
定义,则
2. 期望收益
在这样一个“随机”的博弈中,收益如何计算呢?这就需要计算期望的收益了。期望的收益就是纯策略的博弈结果的收益乘上这个结果出现的概率,对每个博弈结果进行求和。
给定一个策略式博弈和一个混合策略博弈结果
,玩家
的期望收益是
(假设每个玩家的决策是独立的,因此是每个玩家的相应策略的概率乘积)
3. 形式化——混合策略博弈
4. 例子
在下面的博弈中,假设是策略U和策略L的概率,那么:

三、混合策略纳什均衡
1. 定义:混合策略纳什均衡(MNE)
一个混合策略博弈结果是一个混合策略纳什均衡(mixed strategy Nash equilibrium),当对于每个玩家
,都有:
通俗地解释就是:每个玩家都选择在对手不改变的情况下的最好的分布
简写为:MNE
2. 最优反应
玩家的最优反应
定理:是MNE当且仅当对于所有的
,
3. 存在性:纳什定理
定理:有限的策略式博弈一定存在混合策略纳什均衡
有限指:有限的玩家,每个玩家都有有限种纯策略。
4、求解混合策略纳什均衡
定理:是MNE当且仅当玩家
的每个具有正概率的纯策略都是
的最优反应。(证明略)
也就是说,玩家选任意一种纯策略的期望收益是相同的。
用这个定理来求解MNE
例子
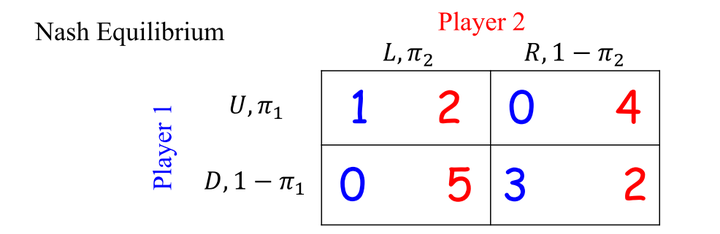
设玩家1选择U的概率是,玩家2选择L的概率是
由玩家2选L的期望收益等于玩家2选R的期望收益,得式子: 由玩家1选U的期望收益等于玩家1选D的期望收益,得式子:
解得:
因此求得纳什均衡
解释
”玩家**选任意一种纯策略的期望收益是相同的“**也可以这么想:如果玩家
的纯策略的期望收益不同的话,那么他会一直选期望收益高的那个,也就是选择一个纯策略,而不是混合策略。这样就回到了纯策略博弈的时代,开篇的例子又说明了有些博弈是找不到纯策略的均衡的。
因此,如果想保持一种”稳定“的局面,每个玩家都没有动机改变当前的策略(或分布),就要保证它选择每个策略的期望收益都相同。
四、小结
本篇内容有:
- 混合策略博弈的定义
- 混合策略纳什均衡的定义及求解
博弈论笔记三:占优策略均衡和理性化
一、占优策略(Dominant Strategy)
1. 例子
在囚徒困境中,收益矩阵是这样的:
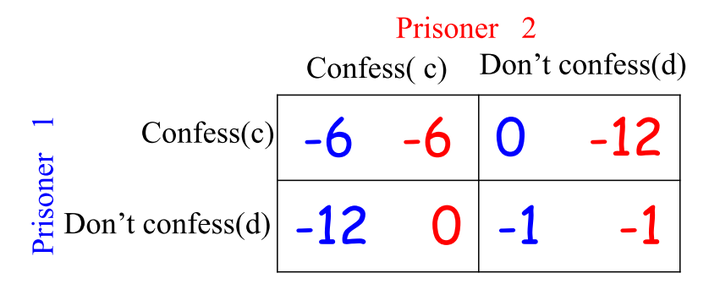
- 当玩家2选择confess的时候,玩家1选confess是最优的;
- 当玩家2选择don’t confess的时候,玩家1选confess是最优的;
可以发现,不管玩家2如何选择,玩家1选择(confess)都是最优的。那么,对于玩家1来说,confess这个策略就是占优策略。
2. 形式化定义
沿用策略式博弈的记号,定义:
- 严格占优于:
和
是一个玩家的两种纯策略,若对于所有
,
,则称策略
严格占优于
- 弱占优于:
和
是一个玩家的两种纯策略,若对于所有
,
,且对于某些
,
,则称策略
弱占优于
- 严格占优策略:如果
严格占优于玩家
其他所有策略,则称
是严格占优策略。
- 弱占优策略:如果
弱占优于玩家
其他所有策略,则称
是弱占优策略。
严格占优就是收益高于其他策略;弱占优就是收益不低于其他策略,且有时高于其他策略。
二、占优策略均衡
定义:每个玩家的占优策略(严格占优策略或弱占优策略)构成的博弈结果,称为占优策略均衡。
从定义可以看出,占优策略均衡属于纳什均衡。
性质:易求解,但可能不存在。
三、例:第二价格拍卖(维克里拍卖)
N个买家通过密封投标的方式竞价,出价最高的投标者获得被拍卖的商品,并支付第二高的出价。竞品对玩家的价值是
,玩家
的出价是
。
玩家的收益:
定理:在第二价格拍卖中,对于任意玩家,策略
是一个弱占优策略,即,
是一个占优策略均衡。
证明:即需证明对于任意,
,分情况讨论如下:
- 如果某人的竞价
-
- 玩家
若想竞拍成功,则
的收益小于0,不如选
的策略(收益为0)。
- 玩家
若竞拍不成功,收益为0,和
的策略相同。
- 玩家
- 如果所有人的竞价
-
- 玩家
若竞拍成功,则收益大于0,收益取决于
的最大值(第二价格),因此,没有比
更好的选择了
- 竞拍不成功,收益为0,不如
的策略
- 玩家
四、被占优策略(Dominated Strategies)
严格占优于
,称
被
严格占优。
弱占优于
,称
被
弱占优。
1. 消除被占优策略可以用来求解占优策略均衡(迭代)
例:
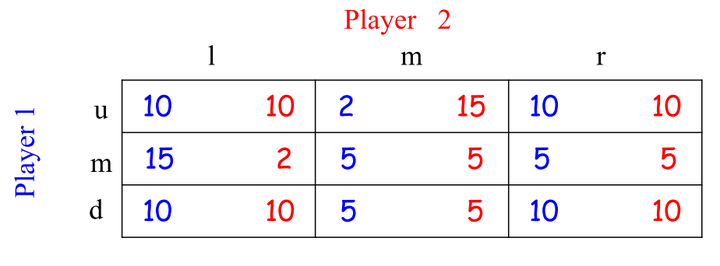
- 对于玩家1:‘u’策略被‘d’策略弱占优。
- 对于玩家2:‘l’策略被‘r’策略弱占优。
消除被占优策略‘u’和‘l’,得:
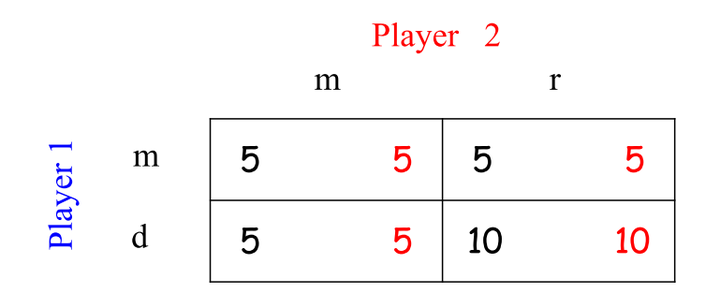
- 对于玩家1:‘m’策略被‘d’策略弱占优。
- 消去玩家1的‘m’策略后,对于玩家2:‘m’策略被‘r’策略严格占优。
最后,得到(d,r)是占优策略均衡(弱占优策略均衡)
2. 消除被占优策略可以用来简化混合策略纳什均衡(MNE)求解
一个策略可以被一个“混合策略”占优,如:
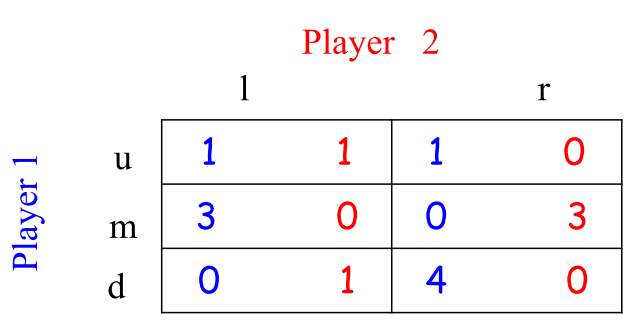
对于玩家1,没有纯策略能够占优于策略‘u’,但是不难看出混合策略严格占优于纯策略‘u’,更一般地,设玩家2的混合策略是
,也就是以概率p选择l策略。
则玩家1在三种纯策略上的收益为: 画图如下:
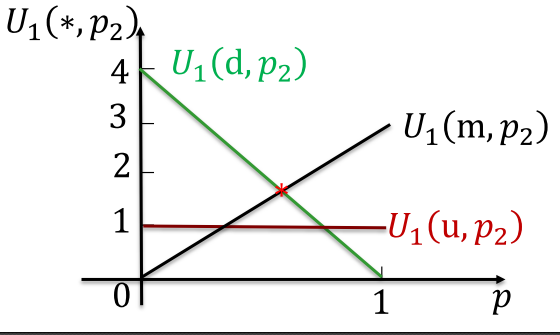
可见,‘u’这个策略始终都不是最好的策略。
定理:被严格占优的策略在MNE中概率为0
证明:
- 笔记(二)MNE那一节讲过,每个具有正概率的纯策略都是
的最优反应,也就是玩家
选任意一种纯策略的期望收益是相同的。
- 但是,因为
被
严格占优,因此
,因此,MNE中,
的概率为0
利用这一定理,可以消去被严格占优的策略,简化MNE的求解。
五、信念和理性化
1. 信念(belief)
定义:“信念”的意思,就是认为对手会采用什么样的策略。对于混合策略博弈,博弈结果,其中,
称为信念(belief)
2. 理性
纯策略是理性的,当:存在信念
使得
是
的最优反应。
定理:在MNE中,每一个具有正概率的纯策略都是理性的。
定理:是理性的当且仅当
不被严格占优。
3. 理性化
理性化:迭代消除被严格占优的策略直到没有被严格占优的策略。
六、例:选美比赛博弈(Beauty Contest game)
- n个玩家
- 每个人选[0,50]之间的一个数
- 玩家
的收益是:
,即与平均数的
越接近,收益越高。
分析:
给定对手的策略,玩家
的最优反应:
可以发现:
这时,在
之间的策略都被严格占优,消去。
迭代理性化,第k次会得到区间:
一直迭代下去,最终得到结果:0
因此,纳什均衡是每个人的策略都是选0
博弈论笔记四:连续博弈
前面讲过了:策略式博弈以及它的纳什均衡。其中,纳什均衡的存在性是由纳什定理保证的(在笔记二讲过):有限的策略式博弈一定存在混合策略纳什均衡。
纳什定理的限制条件是“有限的”策略式博弈。有限是指每个玩家都有有限种纯策略。
现在在策略式博弈中,加入其他的约束条件,纳什均衡的存在性也会得到保证。连续博弈就是加入了这些约束条件的策略式博弈。具体来说,这些约束条件是对策略集和收益函数的约束。
一、连续博弈定义
连续博弈是一种满足某些约束的策略式博弈,约束为:
- 策略集
是非空的紧集
- 收益函数
是连续的
二、定理
1. 纳什定理(回顾)
有限的策略式博弈一定存在混合策略纳什均衡
2. 无限博弈纯策略纳什均衡存在定理
若策略式博弈对于每个
都满足:
是紧集,凸集
在
上连续
在
上是连续的、紧致(concave)的
那么存在纯策略纳什均衡。
3. 无限博弈混合策略纳什均衡存在定理
若策略式博弈对于每个
都满足:
是紧集,凸集
在
上连续
那么存在混合策略纳什均衡。
上面两个定理需要满足的条件我不懂,数学基础比较薄弱……
三、求解纳什均衡
求解纳什均衡,就是这两个步骤:
- 找到最优反应函数
- 找到同时满足所有玩家最优反应函数的解
四、总结
这节课没有什么新的内容,主要是例题,比如古诺模型(Cournot),伯特兰德模型(Bertrand),还有一些其他的。现在比较懒不想写……
博弈论笔记五:相关均衡
纳什均衡中,每个玩家独立地进行策略选择。然而,这种方式有时并不会达到很好的收益,很多坏的策略也会被选到。其实,玩家可以“约定”一下,不去选择坏的结果,这样会提高收益。
相关策略中,玩家的策略选择不是独立的。和混合策略在每个玩家的策略集上加上概率分布不同,相关策略是在所有玩家的策略组合上加上概率分布。
一、引入相关均衡
1. 性别战
收益矩阵如下:策略Ballet和Football分别用B、F代替

根据之前的学习,不难求出纯策略纳什均衡和混合策略纳什均衡。
纯策略纳什均衡:{(B, B), (F, F)},收益分别为(1, 4)和(4, 1)
混合策略纳什均衡:Boy以1/5的概率选择B,以4/5的概率选择F;Boy以4/5的概率选择B,以1/5的概率选择F;期望收益为:(4/5, 4/5)。这个收益比纯策略纳什均衡最坏情况还要低。
现在考虑一个约定:掷一枚均匀的硬币,根据掷硬币的结果来告诉玩家应该选择那种策略。例如,若硬币是正面,那Boy就被告知应该选择B,Girl被告知应该选择B;若硬币是反面,那Boy就被告知应该选择F,Girl被告知应该选择F。也就是(B, B), (F, F)这两种博弈结果都以1/2的概率出现。
如果这个约定能被两人遵守的话,那么收益将会是(5/2, 5/2),比混合策略纳什均衡好很多。
关键点就在于:没有人有违背约定的动机。在上面的例子里,假设Boy单方面违背约定,在硬币正面的时候,选择了F策略,那么,博弈结果将会是(F, B),Boy的收益是0。如果遵守约定,收益将会是1。因此,当违背约定的期望收益不如遵守约定时,所有玩家就都会遵守约定了,这就是相关均衡。
2. 十字路口博弈
这是一个更复杂一点的例子。在一个十字路口有A、B两车,如下右图所示。A有上(U)、下(D)两种策略,B有左(L)、右®两种策略。如果A选择U,B选择R,就“撞车”了,收益为(0, 0),其余收益就不多解释了,如下左图所示。
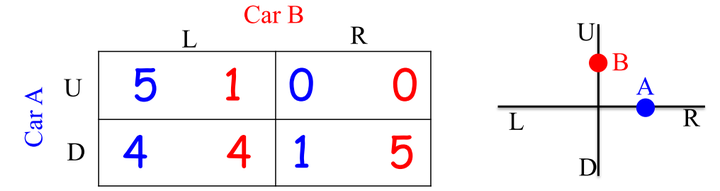
纯策略纳什均衡是(U, L)和(D, R)
混合策略那是均衡是A以1/2的概率选择U,B以1/2的概率选择L。收益为(5/2, 5/2)
第一种约定
现在假设有一个“信号灯”,以均等概率产生“红“、“绿”两种颜色。约定:如果是绿色,A选择U、B选择L;如果是红色,A选择D,B选择R。也就是(U, L)和(D, R)这两种博弈结果都以1/2的概率出现。
如果遵守约定,两人的期望收益为:(3, 3),高于混合策略博弈。
没有玩家会违背约定:如果A看见信号等是绿色,也就是他被告知选择U,B被告知选择L。如果A遵守约定,收益是5;如果A违背约定,博弈结果变为(D, L),收益将会是4。其他情况与此类似。
第二种约定
还可以有另一种约定:”信号灯“以相同的概率(1/3)产生(U, L)、(D, L)和(D, R)这三种结果中的一种,并告知两个玩家应该选择的策略。
期望收益为:(10/3, 10/3)
下面来说明为什么不会违背约定:
- 如果A被告知应该选择U,那么信号灯产生的就是(U, L)这种结果,B被告知选择L。如果A遵守约定,那么A的收益为5;如果A单方面违背约定,那么A的期望收益为4。(博弈结果变为(D, L))。
- 如果A被告知应该选择D,那么信号灯产生的就是(D, L)或者(D, R)的博弈结果,且出现概率均等。即B有1/2的概率被告知选择L,1/2的概率被告知选择R。如果A遵守约定,那么A的收益为5/2;如果A单方面违背约定,那么A的期望收益也为5/2。
A违背约定收益并不会变高,因此没有动机违背约定。
二、相关策略
相关策略就是在博弈结果上加上分布。
表示在策略集
上的概率分布。
就是一个相关策略。
用表示在A上的这个随机变量。
要清楚纯策略、混合策略、相关策略的区别。
例子

对于混合策略,在四种可能的博弈结果上都有一个概率。混合策略:

- 纯策略(B, F)用混合策略表示就是:
- 混合策略
用混合策略表示就是
混合策略一定可以用相关策略表示,但相关策略不一定能用混合策略表示出来。
三、相关均衡
1. 原理解释
相关均衡的概率分布不是随便的,在一定的分布下才会造成相关均衡。什么时候会保持相关均衡呢?那就是每个人都没有动机偏离约定的选择的时候。也就是,当玩家被告知选择策略
的时候,他选择
的期望收益高于选择任何策略
的期望收益。
- 如果玩家
不偏离约定策略
,玩家
的期望收益为:
- 如果玩家
骗了了约定策略,选择了
策略,那么博弈结果会变为
,这个博弈结果出现的概率为
,也就是
的概率,因为只是玩家
改变了应该选择的策略。因此期望收益为:
当不偏离约定的期望收益大于等于偏离约定的期望收益时,就构成了相关均衡。
2. 形式化
策略式博弈的相关均衡是一个联合概率分布
,使得对于任何
,都有:
也可以写成:
3. 例子:计算相关均衡
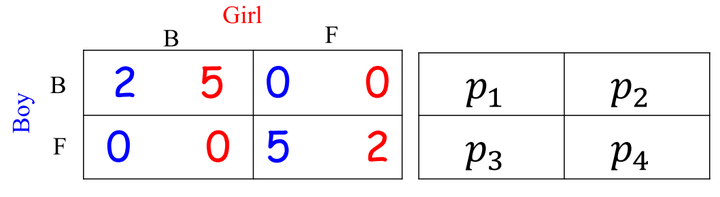
根据上面的公式,可以列出下面几个式子:
计算是线性时间的,比混合策略纳什均衡好很多。
4. 一些结论
- 每个混合策略纳什均衡都是一个相关均衡
- 相关均衡的集合是一个凸集。
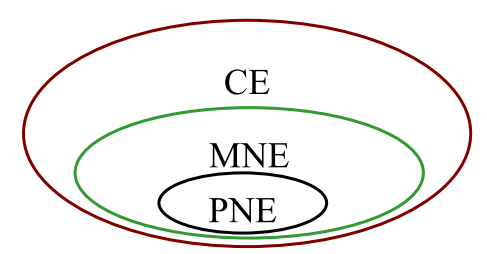
- CE:相关均衡
- MNE:混合策略纳什均衡
- PNE:纯策略纳什均衡
四、总结
这节讲相关均衡,最难的点就在于理解这个均衡。理解了为什么不会偏离“约定”,计算相关均衡就很简单了。
博弈论笔记(六):非完全信息策略式博弈
前面的五节笔记讲的都是完全信息的策略式博弈,而这一章才开始一个新的类别——非完全信息策略式博弈。
一、引言:非完全信息
在一场博弈中,玩家可能并不知道其他玩家的收益、偏好等等。这些情况下的博弈,称为非完全信息的博弈(Incomplete Information)。在非完全信息策略式博弈中,我们考虑一种情况:玩家有一个隐藏的“状态”,在不同的状态下,收益矩阵不同。其他的非完全信息策略式博弈都可以转化为这种模型。
二、例:(非完全信息)
男生和女生决定去看足球(F)还是去看芭蕾(B),如果两个人都知道对方喜欢自己,那么这是一个完全信息博弈,收益矩阵是这样的:
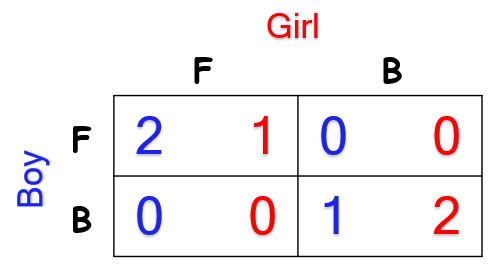
现在假设这样的情况:女生知道男生喜欢她,但是男生却不知道女生的意愿(女生自己是知道的)。不过,男生也并不是一点信息都没有,他知道女生喜欢他的概率为p。这样,收益矩阵就变成了:
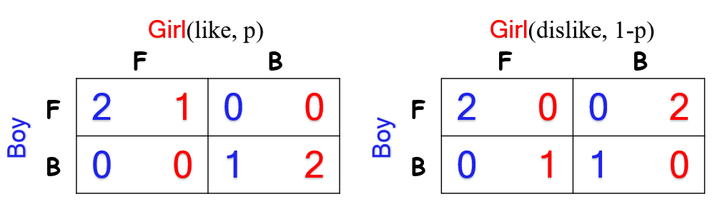
这样的话,如何计算纳什均衡呢?
如果Boy选择F,Girl在喜欢的状态下,F是最优反应,在不喜欢的状态下,B是最优反应。这个时候,如果F是Boy的最优反应,那么(F,(F,B))就构成纳什均衡了。
那么,F是不是Boy的最优反应?什么时候才是Boy的最优反应呢?这就要计算Boy选择F时候的期望收益。Boy如果选择F,有p的概率收益是2,有1-p的概率收益是0。因此,期望收益为: 在其他玩家策略不变的情况下,玩家收益最大的策略是最优反应。上面已经计算了Boy选择F的期望收益,现在要计算在女生策略不变的情况下,Boy选择策略B的收益:
因此,当
也就是
时,
是纳什均衡。
同理,讨论Boy选B的情况,先计算女生的最优反应,再计算男生的最优反应,计算出p的范围是多少的时候,会有纳什均衡。结果是时,
是纳什均衡。
三、形式化:贝叶斯博弈(Bayesian Games)
策略式博弈是贝叶斯博弈,其中:
是玩家集
是策略集
是状态集,表示每个人的私有的信息。给定状态,收益是确定的。
表示在
上的联合分布。
- 玩家
的纯策略
,表示在玩家
的所有状态下的策略选择。
,(假设有
种状态)
- 收益函数
。
表示在这些博弈结果和这些状态下的收益。
这里面,需要仔细说说,它表示每个人的隐藏的状态信息,每个玩家知道自己的状态,但是不知道其他人的状态。如果所有人都只有一个状态,那么就是完全信息的。一般来说,我们研究状态独立的情形,每个人的状态都是独立的,也就是
。
根据贝叶斯规则,有 其中
博弈结果
给定,玩家
的期望收益:
意思:在当前的状态
下,对手的某种状态的概率,乘以这种状态下他们的策略选择的收益,求和。
四、贝叶斯纳什均衡
若博弈结果对于所有的
和
,满足:
则称这个博弈结果是纳什均衡。
最优反应函数
玩家的在给定
和
的最优反应为:
定理
博弈结果是纳什均衡当且仅当对于每个
和
,都有
五、例子:古诺模型(非完全信息)
上面性别战是离散的例子,这里举一个古诺模型。
有两家公司生产同一种商品,这种商品的成本可能有两种:高价和低价
,公司1的成本是
,这是众所周知的。然而公司1不知道公司2的成本是
还是
,它相信公司2成本是
的概率是
。市场上可以卖出的商品单价是(
商品总产量),现在两家公司需要决定各自的产量。
建模:
,
,
- 单价:
或
求解纳什均衡:
对于公司1,求它的期望收益(公司1以p的概率相信公司2是):
对于公司2,如果它成本是
,则期望收益为:
对于公司2,如果它成本是
,则期望收益为:
用期望收益对产量求导等于零,得出收益的极大值点,也就是最优反应函数:
求得纳什均衡:
六、总结
这一节讲了非完全信息策略式博弈,主要是多了"私有状态"这一个概念。状态多的时候,纳什均衡很难求。
博弈论笔记(七):扩展式博弈(Extensive Game)
前面讲过了完全信息策略式博弈、非完全信息策略式博弈。
在策略式博弈中,所有玩家在同一时间做出决策。
扩展式博弈(Extensive Game),也叫动态博弈。和策略式博弈最大的不同,就是玩家是轮流做决策的。
例子:①尼姆游戏:有n枚硬币,两个玩家轮流取硬币,每次可以取1枚或两枚硬币,取到最后一枚硬币的人获胜。②下棋。
特点是:每一步没有收益,只有最后一步,才有收益(获胜)。扩展式博弈相较于策略式博弈,多了玩家的序列信息,以及每个点上的策略集
分类:完全信息扩展式博弈、非完全信息扩展式博弈。
一、一个例子
谷歌想进入中国市场,百度可以选择“对立(F)”和“合作©”
这样可以画出一颗“博弈树”:
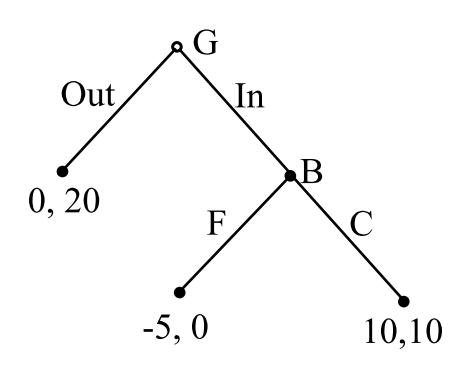
二、表示形式:博弈树
博弈树由结点(node)和边(edge)组成,对应博弈玩家、策略和收益。
- 结点:
- 非叶子结点:代表博弈玩家,表示这个时候哪个博弈玩家做出决策。每个非叶子结点有且仅有一个博弈玩家。
- 叶子结点:代表每个玩家在此时的收益。收益只存在于叶子结点。
- 边:表示策略
三、扩展式博弈形式化定义
- 玩家集N
- 策略集A:表示所有可能的策略。不过在一些结点上可能只有一部分可以选择的策略。
- 历史集H:“策略的序列”构成的集合,可以是有限集或者无限集。H中的元素称为历史(history)。性质:
-
,表示博弈树的根结点。
- 如果策略序列
且
,那么
- 如果无穷策略序列
满足对于任意的
,
,那么
- 每一条历史序列都对应博弈树的一个结点,对应历史序列末端到达的结点。
- 在完全信息扩展式博弈中,历史集大小=结点个数。
- 最终历史(Terminal history):如果
且(
或
- 最终历史集(Terminal history set):Z = {All Terminal history},在这些结点上是收益。
- 博弈玩家函数(Player Function)P:
-
,给每一个非终结历史分配玩家集N中的一个元素。
表示在历史h后,轮到哪个玩家做决策。
- 收益函数(Payoff Function)
,表示第i个玩家的收益
形式化:扩展式博弈G (不需要策略集A,用上面四个就可以完全刻画一个扩展式博弈,因为策略都包含在历史里了)
1. 例子:最后通牒博弈
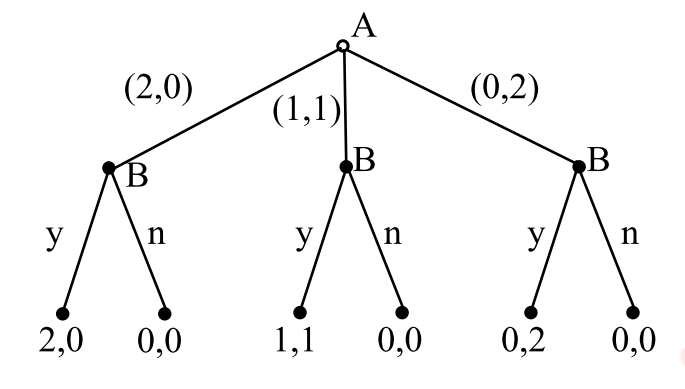
由博弈树转化为扩展式博弈:
2. 例子:由扩展式博弈定义画出博弈树
画出博弈树:
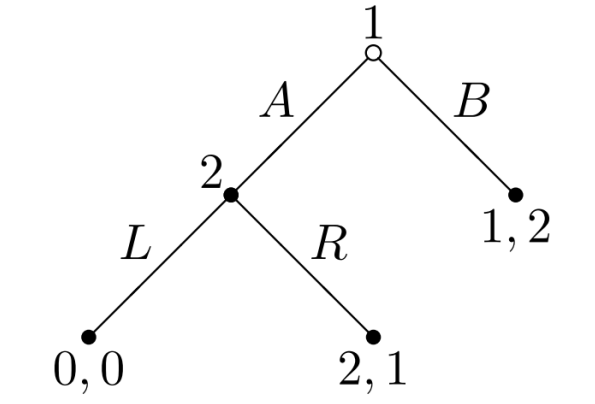
四、扩展式博弈的纯策略(Pure strategies)
给定,玩家
的纯策略的集合是:
通俗地说,就是玩家
的结点上的策略集的笛卡尔积。
例子:最后通牒博弈
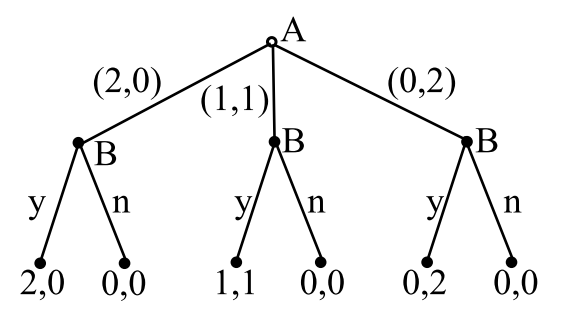
- 玩家A的纯策略:
- 玩家B的纯策略:
例子:
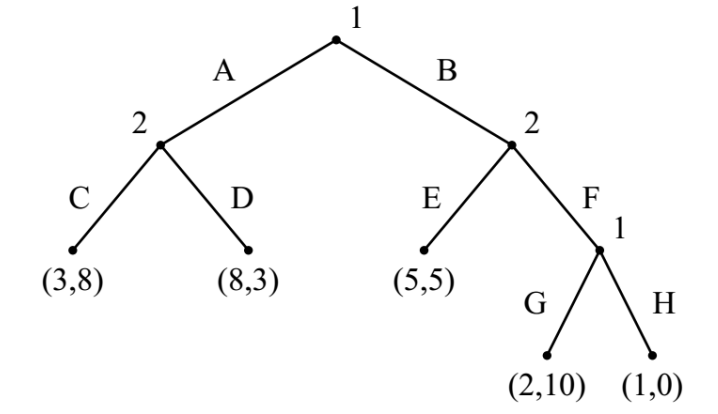
- 玩家1:
- 玩家2:
虽然AG这种纯策略是“不可能”的,因为它们不可能出现在一个历史中,但是这是纯策略的定义。
五、纳什均衡
有了纯策略,就可以定义:混合策略、最优反应、纳什均衡。
和策略式博弈纳什均衡的定义是一样的。
如何求解纳什均衡:诱导策略式博弈
扩展式博弈可以转化为策略式博弈,根据每个玩家纯策略的组合,会出现相应的收益,写出诱导收益矩阵。
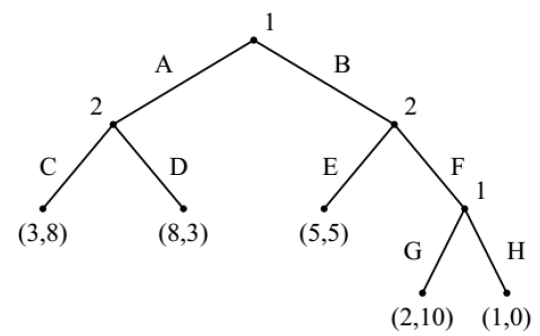
可以转化为:
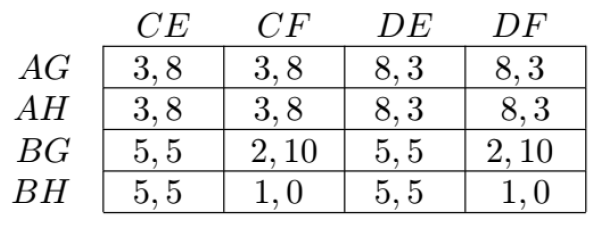
转化不可逆。
根据诱导收益矩阵,就可以找到纳什均衡:(BH, CE),(AG, CF),(AH, CF)
但是,纳什均衡有些策略是不可信的,比如:(AH, CF)是纳什均衡,但A怎么会选择H策略呢?正常一定选G呀。所以,为了避免这些不可信的纳什均衡,需要找出另一种均衡,试所有均衡都是可信的,这就是子博弈完美均衡。
Kuhn Theorem
每一个具有完全信息的有限扩展式博弈至少有一个纯策略纳什均衡(PSNE)
六、子博弈
博弈树的子树,从一个结点开始的所有子结点。
七、子博弈完美纳什均衡(Subgame Perfect Equilibrium)
如果在每个子博弈都是纳什均衡,那么它就是子博弈完美均衡
定理
每一个完全信息扩展式博弈都有子博弈完美均衡。
如何求解子博弈完美均衡?是用后向归纳的方式,从树的叶子端开始,不断剪枝,最终到根节点。具体过程请看下节笔记。
八、小结
这节主要介绍了扩展式博弈的概念、形式化以及纳什均衡。这些都是扩展式博弈的基础的部分。
博弈论笔记(八):求解子博弈完美均衡——单步偏移,后向归纳
一、目标
本节课探究两个目标:
- 子博弈完美均衡(SPE)是否存在?
- 如何找到SPE?
先给出结论:
- 有限的完全信息扩展式博弈,存在SPE
- 计算:后向归纳
二、寻找SPE – 后向归纳
1. 步骤
- 从最末端的非叶子结点开始(从最后的子博弈开始),计算NE(此时对于这个非叶子结点的玩家,相当于寻找他的最优收益)。用这个收益,替代这个子博弈根结点。
- 重复第1步,直到根节点
通过逆向归纳构造的策略博弈集等价于SPE的集合
2. 例子(唯一的SPE)
叶子结点上的收益表示:(1的收益,2的收益)
红色的勾表示选择这个分支。从下往上推,每个人选择自己收益较高的分支。
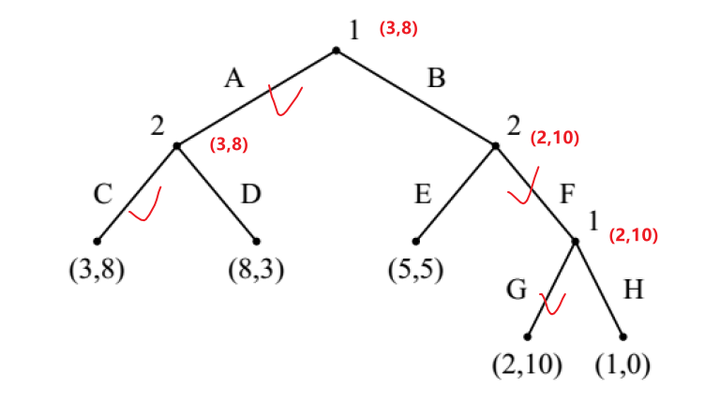
得到SPE:(AG, CF)
3. 例子(不唯一的SPE)
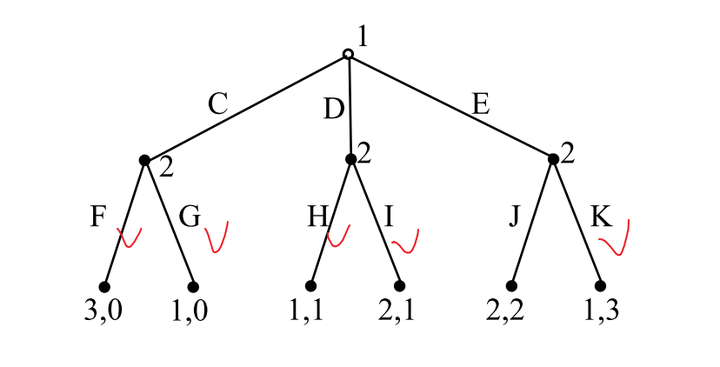
在最高收益相等的时候,根据纳什均衡的定义,这些收益最高的都是纳什均衡。
玩家2会选择的纯策略可能有4种:FHK、FIK、GHK、GIK。当玩家2选择FHK的时候,玩家1在三个分支上的收益分别是:3, 1, 1。因此,玩家1会选择C,得到一个SPE:(C, FHK)。
同理得到所有的SPE:(C, FHK)、(C, FIK)、(C, GHK)、(D, GHK)、(E, GHK)、(D, GIK)
4. 例子(蜈蚣博弈)
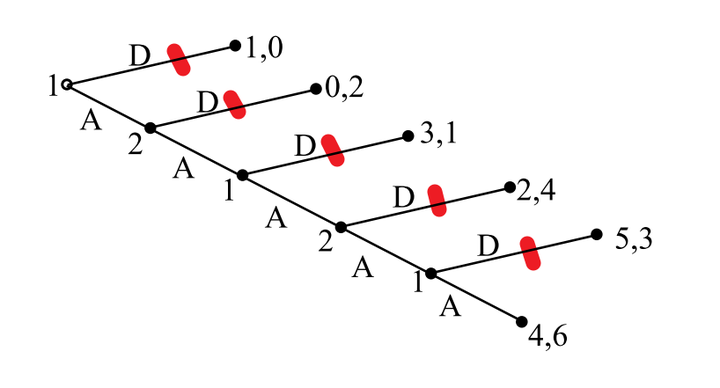
SPE:(DDD, DD)。收益:(1. 0),收益并不理想。
三、形式化之路
如果只是想知道如何求解,形式化似乎不重要。但是如果想严谨地建模,那就必须形式化了。
1. 一些符号记法
- 初始历史:
,表示在结点
的策略集。(不要忘了历史
和结点一一对应)
- 博弈G的长度:
,和树高相同。
:玩家
的某个纯策略
:
and
。(表示在结点
上,玩家
的选择是
,
。)
举例
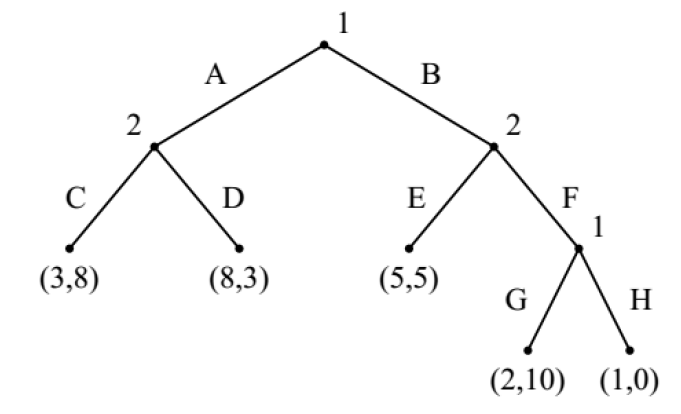
- 设纯策略
,那么
,(在结点BF上,玩家1的选择是G)
2. 定义:有限博弈
博弈G的长度有限。
3. 定义:子博弈
给定,结点h的子博弈定义为:
,其中:
:
,子博弈的历史集
:子博弈中,结点
上的玩家
,子博弈玩家
在历史
的的收益
其他记号:
子博弈中玩家
的纯策略
,子博弈中,玩家
在结点
的策略选择。
4. 定义:子博弈完美均衡(Subgame Perfect Equilibrium)
对于有限博弈,
是子博弈完美均衡(subgame perfect equilibrium),当且仅当:
解释:对于所有子博弈(设根结点是
,根结点上的玩家是
),在子博弈中,玩家
的这种纯策略选择得到的收益,高于其他的纯策略。
5. 单步偏离原则
对于所有子博弈(设子博弈根结点是,根结点上的玩家是
),在子博弈中,玩家
的这种纯策略(记为
)选择得到的收益,不低于那些仅和
在
上不同的纯策略。(也就是只考虑子博弈根节点的策略选择不同)
举例
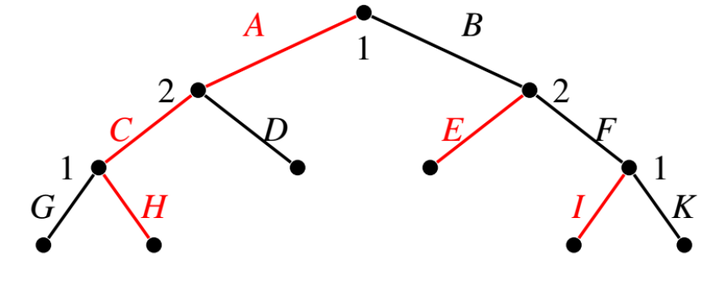
在检验(AHI, CE)是不是SPE的时候,检验根节点的时候,只需比较(AHI, CE)和(BHI, CE)的收益,不需要改变HI, CE。
6. 注意
单步偏离原则不适用于无限博弈
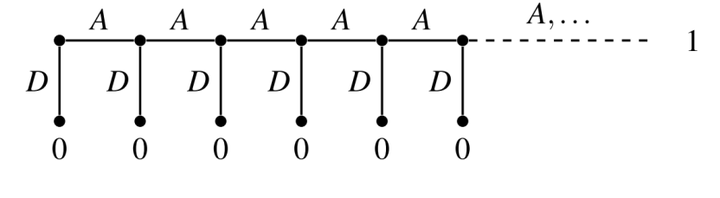
策略DDD……满足单步偏离原则,因为偏离一步之后,收益并没有增加,但是AAA……才是SPE。
7. 库恩定理
每一个具有完全信息的有限扩展式博弈都有子博弈完美均衡。
四、应用
这两道算习题吧。
1. 古诺竞争–主从博弈
古诺竞争已经出现过很多次了,这里再写一下题目:
两个厂商{1, 2}生产和销售同一种商品,厂商
生产的数量记为
。每件商品生产成本都是c,售价是:
和之前不同的是,这次厂商1先决定产量,然后厂商2再决定产量。这就变成了扩展式博弈。求子博弈完美均衡。
求解方法:先求厂商2的最优反应,用表示,然后在求
的最优反应的时候,把
代入,最优反应函数中就只有
这个变量了,然后求极值点,就求出了子博弈完美均衡时的
,再代回求出
。
2. 最后通牒博弈
两人分资产,第一个人选择分给自己的比例。第二个人决定是否同意这种分法。如果同意,二人的收益为
,如果不同意,二人的收益为
,求子博弈完美均衡。
博弈论笔记(九):二人零和博弈
一、形式化定义
二人零和博弈是一个策略式博弈使得对于任意
和
,都有
用语言描述就是:在任何的博弈结果上,两个玩家的收益和都是0。
例子:石头剪刀布,赢的+1分,输的-1分,平局得0分。
可以发现,当一个玩家在一种结果的收益是的时候,另一个玩家的收益一定是
,因此,无需记录两个玩家的收益,只需要记录一个玩家的收益即可。我们按惯例在收益矩阵中保留玩家一的收益。 这个收益矩阵记为u
u 举例如下:
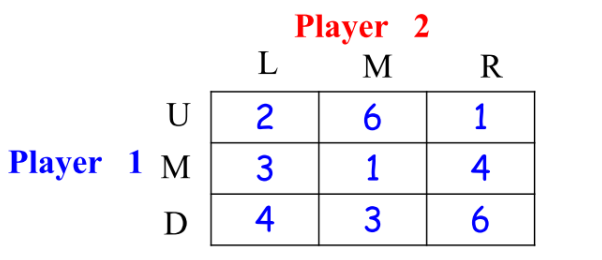 用玩家一的收益表示
用玩家一的收益表示
用之前所学的,寻找最优反应,可以求解二人零和博弈,但是这节讲一种更简单,复杂度更低的求解方法。
二、最大化最小原则(Maxmin)
二人零和博弈也是策略式博弈,当然可以用以前的方法来求解纳什均衡。不过,有了零和的约束,换一种方法去思考会使得求解更为简便。
可以先用策略式博弈的想法开始考虑:
当玩家1固定一个策略时,玩家2会选择对它收益最高的那个策略
,也就是:
对于玩家1,应该采用这样的方法:
把收益矩阵都转化为的形式:
对于玩家一,对每个策略计算最少收益,然后在这些最小值中取最大的。
玩家二收益:
前面的负号不影响策略的取值
三、例子

四、二人零和博弈纳什均衡
定理:对于有限二人零和博弈,玩家1选择策略:
玩家2选择策略:
构成一个纳什均衡 当且仅当
五、混合策略博弈
1. 形式化定义
,其中:
,
是在
上的混合策略(
表示纯策略上的概率分布)
是在
上的混合策略(
表示纯策略上的概率分布)
- 博弈结果:
- 玩家1的期望收益:
,(p,q是行向量)
2. MinMax and MaxMin
类比纯策略,得到
玩家1的选择:
玩家2的选择:
引理:max min ![[公式]](https://www.zhihu.com/equation?tex=%5Cle) min max
min max
二人零和博弈混合策略纳什均衡
定理:对于有限二人零和博弈,玩家1选择策略:
玩家2选择策略:
构成一个混合策略纳什均衡 当且仅当
冯诺依曼最大化最小定理(John von Neumann’s Minimax Theorem)
上面讲了混合策略那是均衡的充要条件,那么混合均衡是否一定存在呢?怎样找到呢?冯诺依曼最大化最小定理给就要给出这两个问题的答案。
定理:
对于有限二人零和博弈,一定有:
即:混合策略纳什均衡一定存在
推论:二人有限零和博弈至少存在一种混合策略纳什均衡:任何一对最优策略都是纳什均衡。
证明:略
根据之前几节学习的,策略式博弈的混合策略纳什均衡一定是存在的,不过那是后来Nash提出来的,运用了更高级的数学工具(不动点定理等),而最大化最小定理是在之前几十年提出的,没有相应的数学工具,所以只能是对二人零和博弈的证明。
在求解上,之前的混合策略纳什均衡求解是NP-Hard问题,而最大化最小定理的求解是一个多项式时间可以求出的。
求解MNE
既然一定存在MNE,那么直接求解最优化问题或者
就可以求出MNE的解。
求解:
令 ,求解
。
是一个固定的行向量,
是一个概率分布,因此,
的最小值就是
向量中最小的那个数。因此:
求解等价于求解线性规划问题:
s.t.
求解等价于求解线性规划问题:
s.t
六、总结
二人零和博弈是策略式博弈的一种特殊情况,普通的混合策略博弈求解难度随着博弈策略呈指数级增加,而二人零和博弈有高效的求解方法,是一个线性规划问题。





