各类损失函数
损失函数
损失函数loss function)是用来估量模型的预测值f(x)与真实值Y的不一致程度,它是一个非负实值函数,通常使用L(Y, f(x))来表示,损失函数越小,模型的鲁棒性就越好。损失函数是经验风险函数的核心部分,也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项,通常可以表示成如下式子:

损失函数、代价函数、目标函数之间的关系

常见的损失函数
均方差(Mean Squared Error,MSE)
均方差(Mean Squared Error,MSE)损失是机器学习、深度学习回归任务中最常用的一种损失函数,也称为 L2 Loss。其基本形式如下:

可以看到这个实际上就是均方差损失的形式。也就是说在模型输出与真实值的误差服从高斯分布的假设下,最小化均方差损失函数与极大似然估计本质上是一致的,因此在这个假设能被满足的场景中(比如回归),均方差损失是一个很好的损失函数选择;当这个假设没能被满足的场景中(比如分类),均方差损失不是一个好的选择
平均绝对误差损失(Mean Absolute Error Loss,MAE)
平均绝对误差(Mean Absolute Error Loss,MAE)是另一类常用的损失函数,也称为L1 Loss。其基本形式如下:

MAE与MSE的区别:
- MSE比MAE能够更快收敛:当使用梯度下降算法时,MSE损失的梯度为
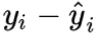 ,而MAE损失的梯度为正负1。所以。MSE的梯度会随着误差大小发生变化,而MAE的梯度一直保持为1,这不利于模型的训练。
,而MAE损失的梯度为正负1。所以。MSE的梯度会随着误差大小发生变化,而MAE的梯度一直保持为1,这不利于模型的训练。 - MAE对异常点更加鲁棒:从损失函数上看,MSE对误差平方化,使得异常点的误差过大;从两个损失函数的假设上看,MSE假设了误差服从高斯分布,MAE假设了误差服从拉普拉斯分布,拉普拉斯分布本身对于异常点更加鲁棒
拉普拉斯分布
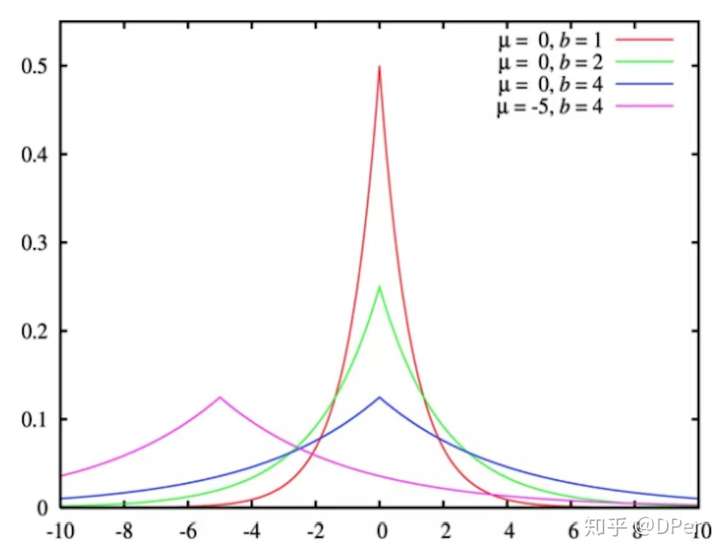
Laplace分布是统计学中的概念,是一种连续的概率分布。如果随机变量的概率密度函数分布为:
么它就是拉普拉斯分布。其中, 是位置参数,
是尺度参数。画出来就是长这样:
高斯分布
高斯分布(正态分布)是一个常见的连续概率分布。正态分布的数学期望值或期望值等于位置参数,决定了分布的位置;其方差的开平方或标准差 等于尺度参数,决定了分布的幅度。正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线(类似于寺庙里的大钟,因此得名)。我们通常所说的标准正态分布是位置参数μ = 0 ,方差σ^2 = 1 的正态分布。


平均绝对误差百分比(Mean Absolute Percentage ErrorAPE,MAPE)
**MAPE(Mean Absolute Percentage Error)平均绝对误差百分比:**是用来做销量预测最常用的指标,在实际的线上线下销量预测中有着非常重要的评估意义。但是在实际的项目过程中发现,有些时候的指标并不能非常好的表示模型拟合的效果,因此对这部分进行了深入分析,发现有更优化的评价指标来度量销量预测问题。
MAPE公式如下:
,
分别为真实值和预测值。
平均平方log误差(Mean Squared Logarithmic Error, MSLE)
1 | msle相比与mse的改进:如果想要预测的值范围很大,mse会受到一些大的值的引导,即使小的值预测准也不行.假设如: |
当目标实现指数增长时,例如人口数量、一种商品在几年时间内的平均销量等,这个指标最适合使用。请注意,这个指标惩罚的是一个被低估的估计大于被高估的估计。
Huber Loss
Huber Loss是一种将MSE与MAE结合起来,取两者优点的损失函数,也被称作Smooth Mean Absolute Error Loss 。其原理很简单,就是在误差接近0时使用MSE,误差较大时使用MAE,公式为:

在 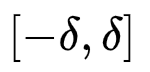 内实际上就是MSE的损失,使损失函数可导并且梯度更加稳定;在
内实际上就是MSE的损失,使损失函数可导并且梯度更加稳定;在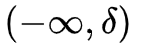 和
和 区间内为MAE损失,降低了异常点的影响,使训练更加鲁棒。
区间内为MAE损失,降低了异常点的影响,使训练更加鲁棒。
回归损失函数:Log-Cosh Loss
Log-Cosh是应用于回归任务中的另一种损失函数,它比L2损失更平滑。Log-cosh是预测误差的双曲余弦的对数。
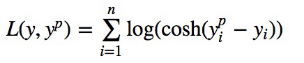

优点:
对于较小的X值,log(cosh(x))约等于(x ** 2) / 2;对于较大的X值,则约等于abs(x) - log(2)。这意味着Log-cosh很大程度上工作原理和平均方误差很像,但偶尔出现错的离谱的预测时对它影响又不是很大。它具备了Huber损失函数的所有优点,但不像Huber损失,它在所有地方都二次可微。
但Log-cosh也不是完美无缺。如果始终出现非常大的偏离目标的预测值时,它就会遭受梯度问题。
Log-cosh损失函数的Python代码:
1 | # log cosh 损失 |
中位数绝对误差(Median absolute error,MAE)
中位数绝对误差适用于包含异常值的数据的衡量。先计算出数据与它们的中位数之间的残差(偏差),MedAE就是这些偏差的绝对值的中位数。
绝对中位差,一种统计离差的测量。而且,是一种鲁棒统计量,比标准差更能适应数据集中的异常值。对于标准差,使用的是数据到均值的距离平方,所以大的偏差权重更大,异常值对结果也会产生重要影响。对于绝对中位差,少量的异常值不会影响最终的结果。
由于绝对中位差是一个比样本方差或者标准差更鲁棒的度量,它对于不存在均值或者方差的分布效果更好,比如柯西分布。
explained_variance_score(解释方差分)
解释回归模型的方差得分,这个指标用来衡量我们模型对数据集波动的解释程度,其值取值范围是[0,1],越接近于1说明自变量越能解释因变量的方差变化,值越小说明效果越差。
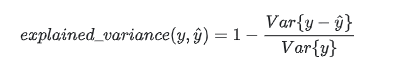
分位数损失(Quantile Loss)
分位数回归Quantile Regression是一类在实际应用中非常有用的回归算法,通常的回归算法是拟合目标值的期望(MSE)或者中位数(MAE),而分位数回归可以通过给定不同的分位点,拟合目标值的不同分位数。
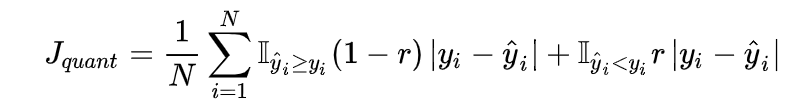
式中的r为分位数,这个损失函数是一个分段的函数,当r>0.5时,低估()的损失要比高估的损失更大;反之,当r<0.5 时,高估的损失要比低估的损失更大,分位数损失实现了分别用不同的系数控制高估和低估的损失,进而实现分位数回归。特别地,当r=0.5时,分位数损失退化为MAE损失,从这里可以看出 MAE 损失实际上是分位数损失的一个特例—中位数回归。

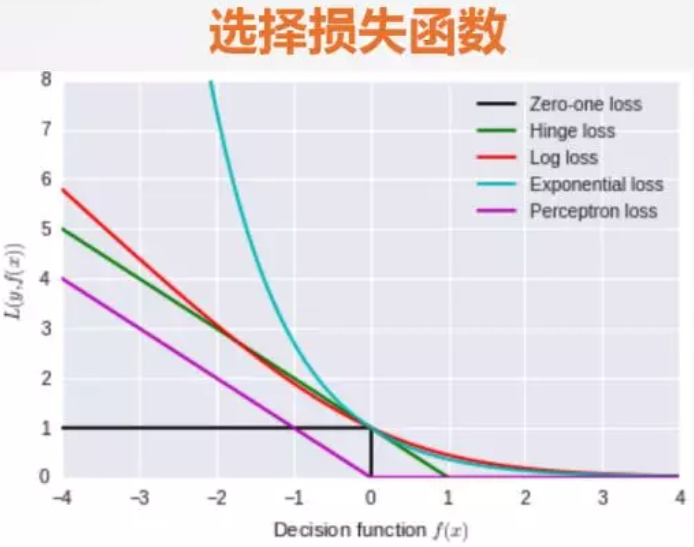
分类常用的损失函数
0-1损失函数(zero-one loss)

log对数损失函数

指数损失函数(exponential loss)

hinge损失函数
支持向量机Support Vector Machine (SVM)模型的损失函数本质上就是Hinge Loss + L2正则化。

交叉熵损失函数 (Cross-entropy loss function)

多分类问题的交叉熵损失函数

相对熵
KL距离全称为Kullback-Leibler Divergence,也被称为相对熵。公式为:

感性的理解,KL距离可以解释为在相同的事件空间P(x)中两个概率P(x)和Q(x)分布的差异情况。
从其物理意义上分析:可解释为在相同事件空间里,概率分布P(x)的事件空间,若用概率分布Q(x)编码时,平均每个基本事件(符号)编码长度增加了多少比特。

如上面展开公式所示,前面一项是在P(x)概率分布下的熵的负数,而熵是用来表示在此概率分布下,平均每个事件需要多少比特编码。这样就不难理解上述物理意义的编码的概念了。
但是KL距离并不是传统意义上的距离。
传统意义上的距离需要满足三个条件:
-
1)非负性;
-
2)对称性(不满足);
-
3)三角不等式(不满足)。
但是KL距离三个都不满足。





