层次分析法(AHP)

定义：

通过构建一套多层次的评价指标体系，完成对定性指标的定量化分析。

运用范围：

运用于多目标、多准则、多要素、多层次的非结构化的复杂决策问题，特别是战略决策问题，可以较好地解决多要素相互关联、相互制约的复杂系统的评价。

比如： 旅游出行，评定信用，多角度评价产品优劣。

举个栗子：如TA爱你的程度，可以用联系你的频率、关心你的程度、为你付出时间、为你付出的购买力等因素。先对这几个指标进行权重赋值，随后结合你的TA这些指标相应的得分，进行权重*得分的乘积运算，并将所有要素进行加和，即可得到TA爱你的程度（指数，手动狗头·-·）

在实际工作中，层次分析法经常和德尔菲法、百分权重法结合，用于确定评价指标的权重。

历史案例

1971年AHP首次应用于美国国防部研究“应急计划”，随后又开展了多项研究，奠定了AHP在定性研究领域的基础，1982年AHP在“中美能源、资源、环境”学术会议上被首次介绍到中国。

喵博士结合相关研究现状，梳理了当前主要涉及领域应用如下：适宜性评价、环境保护措施评价、安全性评价、危化物危害性评价、城市应急灾害能力评价、空间格局安全性评价。同时，亦可用于指导消费者在生活领域决策提供一定指导，如购房影响因素评价、购车影响因素评价、专业选择与就业倾向评价等，均可以发挥其优秀的功效。

如在居住区适宜性评价（如上图）时，根据既有研究成效，居住区园林景观适宜性评价可以划分为：绿化种植景观、道路景观、场所景观、硬质景观、水景景观和庇护性景观等六个一级指标（准则层），每个一级指标又可以细分为若干二级指标，以完成定性指标的定量化分析。

分析方法

基于层次分析法（AHP）先分解后综合的基本工作思路，先将要分析的要素进行层次化、步骤化，构建形成多层次分析评价模型，最终确定各层级指标的重要程度（权重），或优先次序。

AHP把一个复杂的问题表示为一个有序的递阶层次结构，并通过主管判断和科学计算给出备选方案的优劣顺序（或权重）。简而言之，层次分析法人如其名，首先要构建合理的层次，其次要分析层次内部各因素的优劣。

层次分析法的使用流程：

1. 根据需求对目标层进行分解，如适宜性可以分解为6个一级指标；

2. 建立层次结构图，及判断矩阵；

3. 计算权重系数（主要基于德尔菲法，或曰专家打分，对各指标要素的权重进行赋值）；

4. 进行一致性检验（在AHP软件中可自行设定），若一致性指标CR<0.1，则满足研究需要，进入下一环节。不满足时则需要对各指标权重重新赋值（重新进行第三步分析）；

5. 层次总排序，选出最优方案。

分三层一般：目标层，准则层，方案层

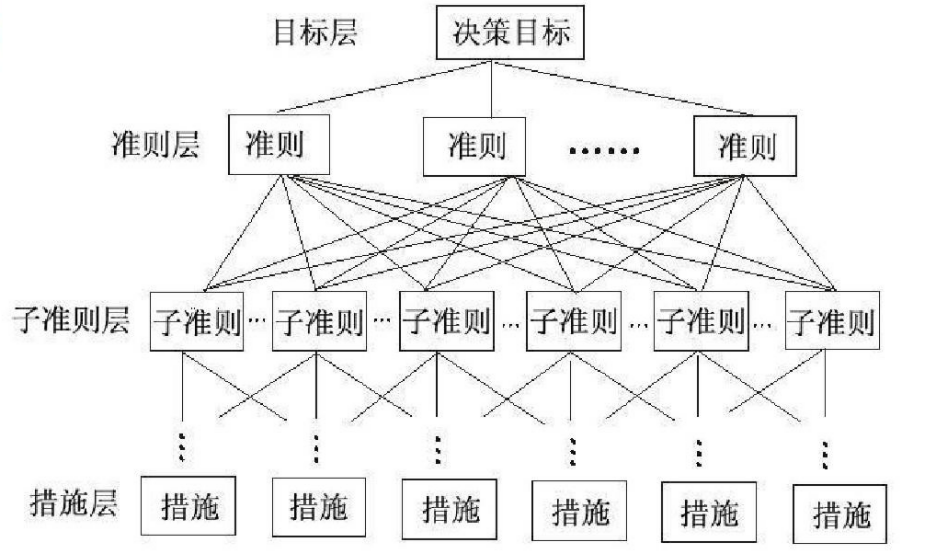
如在评价购房影响要素时，可以细分为房价要素、区位要素、户型要素、口碑要素等一级指标，并分别对各一级要素进行深度开发，构建相应的二级评价指标以完成对一级指标的评价。

步骤分解

1）建立层次结构模型

将决策的目标（城市空间格局安全）、考虑的决策准则因素（空间结构安全、空间要素安全、空间环境安全）和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。

2）构造判断矩阵

在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而Saaty等人提出：一致矩阵法，即：不把所有因素放在一起比较，而是两两相互比较。对比时采用相对尺度，以尽可能减少性质不同因素相互比较的困难，以提高准确度。

由专家对同一层次内N个指标的相对重要性（两两因素之间）进行打分。相对重要性的比例标度取1-9之间。同时，对各同级指标的重要性评价时，存在三种标度范畴（如下图），根据研究需要自行选择。

构建判断矩阵A（正交矩阵），用aij表示第i个因素相对于第j个因素的比较结果：

3) 计算权重

将矩阵A的各行向量进行几何平均（方根法），然后进行归一化，即得到各评价指标权重和特征向量W：

4) 一致性检验

判断矩阵的一致性检验，所谓一致性是指判断思维的逻辑一致性。如当甲比丙是强烈重要，而乙比丙是稍微重要时，显然甲一定比乙重要。这就是判断思维的逻辑一致性，否则判断就会有矛盾。

计算最大特征根λmax：

计算一致性指标CI（Consistency Index）、随机一致性指标RI（Random Index）和一致性比例CR（Consistency Ratio）：

一般情况下，当CR＜0.1时，即认为矩阵具有满意的一致性，否则需要对判断矩阵进行调整。

5）层次排序

层次排序，可分为层次单排序和层次总排序。所谓层次单排序是指，对于上一层某因素而言，本层次各因素的重要性的排序。层次总排序，确定某层所有因素对于总目标相对重要性的排序权值过程，称为层次总排序。这一过程是从最高层到最底层依次进行的。对于最高层而言，其层次单排序的结果也就是总排序的结果。

计算某一层次所有因素对于最高层（目标层）相对重要性的权值，称为层次总排 序。该过程是从最高层次向最低层次依次进行：

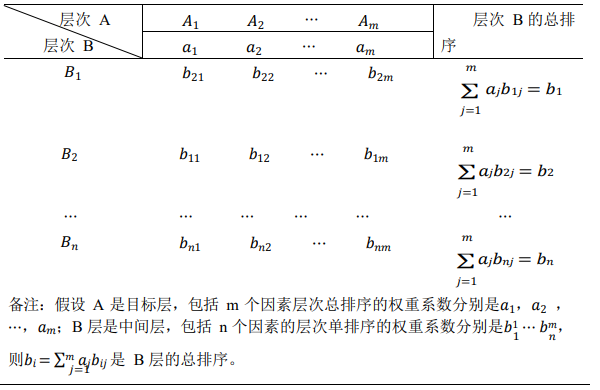
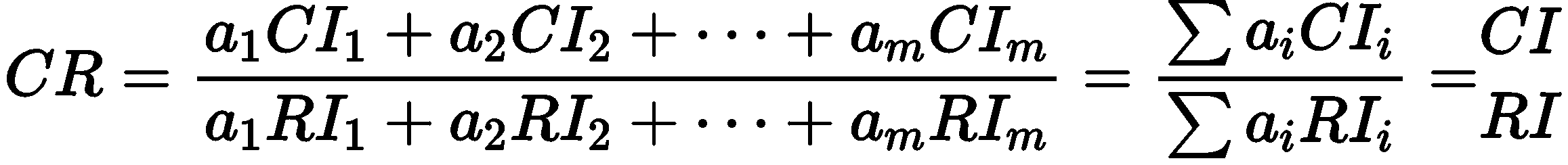
当𝐶𝑅 < 0.1时，认为层次总排序通过一致性检验，否则就需要重新调整判断矩阵 的元素取值。到此，根据最下层（决策层）的层次总排序做出最后的决策。

案例分析

1）构建评价结构

一位顾客决定要买一套新住宅，经过初步调查研究确定了三套候选的房子A、B、C，问题是如何在这三套房子里选自一套较为满意的房子呢? 下面给出有关的数据和资料：

将影响购买新房的因素归纳为4个标准：

· 房子的地理位置及交通；

· 房子的居住环境；

· 房子结构、布局与设施；

· 房子的每平方米建筑面积地单价（模型如下）。

2）邀请专家（20-30名）打分

对同一层次内4个指标的相对重要性（两两因素之间）进行打分。经过专家的打分，每个标准相对的权重，即标准的特征向量如下表。

3）用规范列平均法求权重

第一步：先求出两两比较矩阵每一列的总和。

第二步：把两两比较矩阵的每一元素除以其相应列的总和，所得商所组成的新的矩阵称之为标准两两比较矩阵。

第三步：计算两两比较矩阵的每一行的平均值，这些平均值就是各方案在地理位置及交通方面的权重。

我们称最后求得的行平均值为房子选择问题中地理位置及交通方面的特征向量。三个方案在其它三个方面的特征向量。

每个标准相对的权重，即标准的特征向量。通过两两矩阵比较，可求得标准的特征向量如下：

地理位置及交通：0.398

居住环境：0.218

结构布局设施：0.085

每平米单价：0.299

4）两两比较一致性检验

两两比较矩阵的元素是通过两个因素比较得到的，而在很多这样的比较中，往往可能得到一些不一致性的结论。例如，当因素i、j、k的重要性很接近的时候，在两两比较时，可能得出i比j重要，j比k重要，而k又比i重要等矛盾的结论，这在因素的数目多的时候更容易发生。

第一步：由被检验的两两比较矩阵乘以其特征向量，所得的向量称之为赋权和向量。

第二步:每个赋权和向量的分量分别除以对应的特征向量的分量。

1.803 / 0.593 =3.040

1.034 / 0.341 =3.032

0.197 / 0.066 =2.985

第三步：计算出第二步结果中的平均值，记为λmax。

λmax = (3.040+3.032+2.985)/ 3 = 3.019

第四步：计算一致性指标CI。

CI = (λmax– n ) / (n - 1)

CI = (3.019 – 3 ) / (3 – 1 ) = 0.010

第五步：计算一致性率CR

CR = CI / RI，在这里，RI是自由度指标（修正值）。

本例中可计算得

CR = 0.01 / 0.58 = 0.017 < 0.1

我们已经求出了四个标准的特征向量，以及四个在单一标准下的三个购房方案的特征向量，如表：

5）最优方案求解

方案 A：

0.3980.593+0.2180.123+0.0850.087+0.2990.265=0.349

方案 B（最优）

0.3980.341+0.2180.320+0.0850.274+0.2990.655=0.425

方案 C：

0.3980.066+0.2180.557+0.0850.639+0.2990.080=0.226

优缺点

层次分析法优点：

· 系统性的分析方法

层次分析法把研究对象作为一个系统，按照分解、比较判断、综合的思维方式进行决策，成为继机理分析、统计分析之后发展起来的系统分析的重要工具。系统的思想在于不割断各个因素对结果的影响，而层次分析法中每一层的权重设置最后都会直接或间接影响到结果，而且在每个层次中的每个因素对结果的影响程度都是量化的，非常清晰明确。这种方法尤其可用于对无结构特性的系统评价以及多目标、多准则、多时期等的系统评价。

· 简洁实用的决策方法

这种方法既不单纯追求高深数学，又不片面地注重行为、逻辑、推理，而是把定性方法与定量方法有机地结合起来，使复杂的系统分解，能将人们的思维过程数学化、系统化，便于人们接受，且能把多目标、多准则又难以全部量化处理的决策问题化为多层次单目标问题，通过两两比较确定同一层次元素相对上一层次元素的数量关系后，最后进行简单的数学运算。计算简便，并且所得结果简单明确，容易为决策者了解和掌握。

· 所需定量数据信息较少

层次分析法主要是从评价者对评价问题的本质、要素的理解出发，比一般的定量方法更讲求定性的分析和判断。由于层次分析法是一种模拟人们决策过程的思维方式的一种方法，层次分析法把判断各要素的相对重要性的步骤留给了大脑，只保留人脑对要素的印象，化为简单的权重进行计算。这种思想能处理许多用传统的最优化技术无法着手的实际问题。

层次分析法缺点：

· 不能为决策提供新方法

层次分析法的作用是从备选方案中选择较优者。在应用层次分析法的时候，可能就会有这样一个情况，就是我们自身的创造能力不够，造成了我们尽管在我们想出来的众多方案里选了一个最好的出来，但其效果仍然不够企业所做出来的效果好。而对于大部分决策者来说，如果一种分析工具能替我分析出在我已知的方案里的最优者，然后指出已知方案的不足，又或者甚至再提出改进方案的话，这种分析工具才是比较完美的。但显然，层次分析法还没能做到这点。

· 定量数据较少，定性成分多，不易令人信服

在如今对科学的方法的评价中，一般都认为一门科学需要比较严格的数学论证和完善的定量方法。但现实世界的问题和人脑考虑问题的过程很多时候并不是能简单地用数字来说明一切的。层次分析法是一种带有模拟人脑的决策方式的方法，因此必然带有较多的定性色彩。

· 指标过多时，数据统计量大，且权重难以确定

当我们希望能解决较普遍的问题时，指标的选取数量很可能也就随之增加。指标的增加就意味着我们要构造层次更深、数量更多、规模更庞大的判断矩阵。那么我们就需要对许多的指标进行两两比较的工作。由于一般情况下我们对层次分析法的两两比较是用1至9来说明其相对重要性，如果有越来越多的指标，我们对每两个指标之间的重要程度的判断可能就出现困难了，甚至会对层次单排序和总排序的一致性产生影响，使一致性检验不能通过。不能通过，就需要调整，在指标数量多的时候比较难调整过来。

· 特征值和特征向量的精确求法比较复杂

在求判断矩阵的特征值和特征向量时，所用的方法和我们多元统计所用的方法是一样的。在二阶、三阶的时候，我们还比较容易处理，但随着指标的增加，阶数也随之增加，在计算上也变得越来越困难。不过幸运的是这个缺点比较好解决，我们有三种比较常用的近似计算方法。第一种就是和法，第二种是幂法，还有一种常用方法是根法

公式整理

判断矩阵

$$A=\left(a_{i j}\right)_{n \times n}=\left(\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & \cdots & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right)$$

计算权重

$$\mathrm{w}_{\mathrm{i}}=\overline{\mathrm{W}}_{\mathrm{i}} / \sum_{\mathrm{i}=1}^{\mathrm{n}} \overline{\mathrm{w}}_{\mathrm{i}}, \mathrm{W}=\left\{\begin{array}{c} \mathrm{w}_{1} \\ \mathrm{w}_{2} \\ \cdot \\ \dot{w}_{n} \end{array}\right\}$$

最大特征根

$$\lambda \max =\frac{1}{\mathrm{n}} \sum_{\mathrm{i}=1}^{\mathrm{n}} \frac{(\mathrm{AW})_{\mathrm{i}}}{\mathrm{w}_{\mathrm{i}}}$$

$$\mathrm{CI}=\frac{\lambda \max -\mathrm{n}}{\mathrm{n}-1}$$

参考资料

用人话讲明白AHP层次分析法（非常详细原理+简单工具实现）_Halosec_Wei的博客-CSDN博客_ahp层次分析法

百度百科-层次分析法