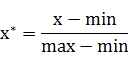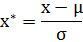正则化(regularization)

正则化的目的

正则化是为了防止过拟合，进而增强泛化能力。
"泛化"指的是一个假设模型能够应用到新样本的能力。

L1 正则化和 L2 正则化的几何含义

L1 正则化通常称为 Lasso 正则化：

$J(θ)=−∑i=1m(y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))))+λm∑j=1n|θj|$

L2 正则化通常称为 Ridge 正则化：

$J(θ)=−∑i=1m(y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))))+λ2m∑j=1nθj2$

我们可以写成统一的形式：

$J(θ,μ)=f(θ)+μh(θ)⇔J(θ,μ)=f(θ)+μ(h(θ)−η)$

其中 η 为常数，不影响最优值的求解。

可以还原为：

$min f(θ)$

$s.t. h(θ)≤η$

那么他们的几何含义是：

对于 L1 正则化 ( Lasso 正则化)：$$ h(θ)=∑j=1n|θj|$$

对于 L2 正则化 ( Ridge 正则化)：$$ h(θ)=∑j=1nθj2$$

Q：以下哪个图形是 L1 正则化，哪个图形是 L2 正则化？

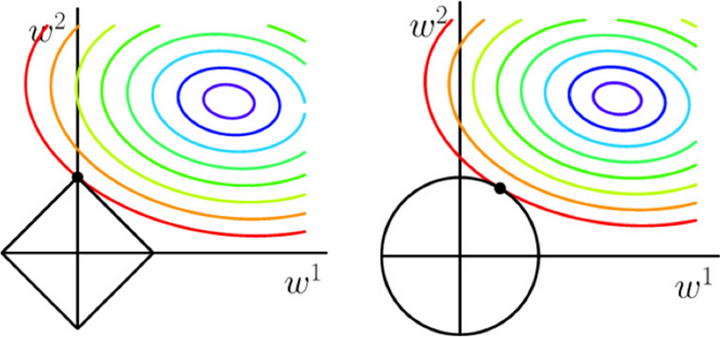
左边的图为 L1 正则化，右图为 L2 正则化。

因为对于 L1 正则化而言 h(θ)=|w1|+|w2|≤η ，在图中表示一个菱形区域。

对于 L2 正则化而言h(θ)=w12+w22≤η，在图中表示一个圆形区域。

L1 正则化和 L2 正则化正则化的推广

逻辑回归正则化可以写成统一的形式 Lq 正则化：
J(θ)=−∑i=1m(y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))))+λ2m∑j=1n|θj|q
其中 q≥0。不同的 q 值对应着不同的约束边界，如下图所示：

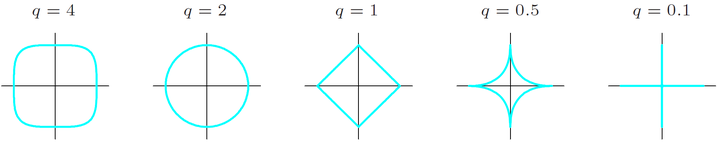
从上图可以看出，

q=1 对应着 L1 正则化， q=2 对应着 L2 正则化。
而当 q<1 时，约束边界为非凸函数，求解最优值非常困难。 q=1 是满足约束边界为凸的最小值。
当 q≤1 时，约束边界在坐标轴上不可导，为非光滑函数，不能用梯度下降法进行求解。
对于 q∈(1,2) 的情况是 L1 正则化和 L2 正则化的折中，同时具有两者的优点。此时的约束边界为凸边界，既具有 L2 正则化的光滑可导性，同时具有 L1 正则化获得稀疏特征的优点。
实践表明，对于q>2 的情况，效果并不会比 q∈[1,2] 好，没必要进行讨论。
Zou 和 Hastie (2005) 引入了 Elastic Net 正则化，可以通过参数 α 调节L1正则化和L2正则化的权重

即

$\frac{\lambda}{2 m} \sum_{j=1}^{n}\left(\alpha \theta^{2}+(1-\alpha)\left|\theta_{j}\right|\right)$

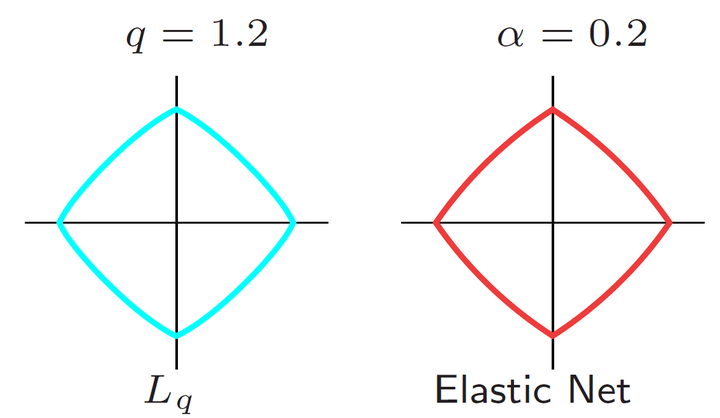
如下图为q=1.2时的Lq正则化和α=0.2 时的 Elastic Net 正则化，两种不同的方式对 L1 正则化和 L2 正则化进行了折中。这两种方法均继承了 L1 正则化获得稀疏矩阵的优点。至于光滑可导性，乍一看二者没什么区别，实际上 Lq 正则化在坐标处是可导的，而 Elastic Net 正则化在坐标处是不可导的。

欢迎关注我的博客：https://2018august.github.io/

离散化

定义

离散化是指将连续的数据进行分段，使其变为一段段离散化的区间。分段的原则有基于等距离、等频率或优化的方法。

作用

模型限制
比如决策树、朴素贝叶斯等算法，都是基于离散型的数据展开的。如果要使用该类算法，必须将离散型的数据进行。有效的离散化能减小算法的时间和空间开销，提高系统对样本的分类聚类能力和抗噪声能力。
离散化的特征更易理解
比如工资收入，月薪2000和月薪20000，从连续型特征来看高低薪的差异还要通过数值层面才能理解，但将其转换为离散型数据(低薪、高薪)，则可以更加直观的表达出了我们心中所想的高薪和低薪。
使模型结果更加稳定

归一化

归一化方法有两种形式，一种是把数变为(0，1)之间的小数，一种是把有量纲表达式变为无量纲表达式。

主要是为了数据处理方便提出来的，把数据映射到0~1范围之内处理，更加便捷快速，应该归到数字信号处理范畴之内。

原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。

min-max标准化（Min-Max Normalization）

也称为离差标准化，是对原始数据的线性变换，使结果值映射到[0 , 1]之间。

使用这种方法目的：
1、对于方差非常小的属性可以增强其稳定性；
2、维持稀疏矩阵中为0的条目。

手写代码实现：

import numpy as np
arr = np.asarray([0, 10, 50, 80, 100])
for x in arr:
	x = float(x - np.min(arr))/(np.max(arr)- np.min(arr))
	print x
 
# output
# 0.0
# 0.1
# 0.5
# 0.8
# 1.0

sklearn代码实现：

from sklearn import preprocessing   
 
import numpy as np  
 
X = np.array  ([[ 1., -1.,  2.],  
				[ 2.,  0.,  0.],  
				[ 0.,  1., -1.]])  
	
min_max_scaler = preprocessing.MinMaxScaler() #MinMaxScalar函数 
X_minMax = min_max_scaler.fit_transform(X)   

X_minMax

# output 
array([ [ 0.5       ,  0.        ,  1.        ],  
		[ 1.        ,  0.5       ,  0.33333333],  
		[ 0.        ,  1.        ,  0.        ]])

当然，在构造类对象的时候也可以直接指定最大最小值的范围：
feature_range=(min, max)，
此时应用的公式变为：

1 2	X_std=(X-X.min(axis=0))/(X.max(axis=0)-X.min(axis=0)) X_minmax=X_std/(X.max(axis=0)-X.min(axis=0))+X.min(axis=0))

Z-score标准化方法(mean normaliztion)

也称为均值归一化(mean normaliztion)，给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1。转化函数为：

其中 μ 为所有样本数据的均值，σ为所有样本数据的标准差。

手写代码实现

import numpy as np
 
arr = np.asarray([0, 10, 50, 80, 100])
for x in arr:
	x = float(x - arr.mean())/arr.std()
	print x
 
# output
# -1.24101045599
# -0.982466610991
# 0.0517087689995
# 0.827340303992
# 1.34442799399

skleran代码实现

1
2
3

from sklearn import preprocessing

data = preprocessing.scale(values) #注意，这里的values是array

函数转换方法

log函数转换

通过以10为底的log函数转换的方法同样可以实现归一下，具体方法如下：

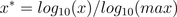
使用注意：max为样本数据最大值，并且所有的数据都要大于等于1。

atan函数转换

通过反正切函数也可以实现数据的归一化：

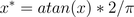
使用这个方法需要注意的是如果想映射的区间为[0,1]，则数据都应该大于等于0，小于0的数据将被映射到[-1,0]区间上，而并非所有数据标准化的结果都映射到[0,1]区间上。

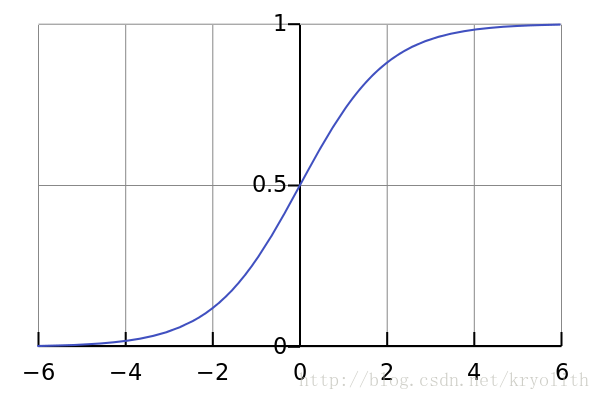
Sigmoid函数转换（十分重要）

Sigmoid函数是一个具有S形曲线的函数，是良好的阈值函数，在(0, 0.5)处中心对称，在(0, 0.5)附近有比较大的斜率，而当数据趋向于正无穷和负无穷的时候，映射出来的值就会无限趋向于1和0，是个人非常喜欢的“归一化方法”，之所以打引号是因为我觉得Sigmoid函数在阈值分割上也有很不错的表现，根据公式的改变，就可以改变分割阈值，这里作为归一化方法，我们只考虑(0, 0.5)作为分割阈值的点的情况：

def sigmoid(X,useStatus):
	if useStatus:
 	    return 1.0 / (1 + np.exp(-float(X)))
	else:
    	return float(X)