链接：

一文读懂残差网络

残差网络的由来

残差操作这一思想起源于论文《Deep Residual Learning for Image Recognition》，目前的引用量已达3万多。这篇文章发现，如果存在某个[公式]层的网络[公式]是当前最优的网络，那么可以构造一个更深的网络，其最后几层仅是该网络[公式]第[公式]层输出的恒等映射(Identity Mapping)，就可以取得与[公式]一致的结果；也许[公式]还不是所谓“最佳层数”，那么更深的网络就可以取得更好的结果。总而言之，与浅层网络相比，更深的网络的表现不应该更差。但是如下图所示，56层的神经网络表现明显要比20层的差。证明更深的网络在训练过程中的难度更大，因此作者提出了残差网络的思想。

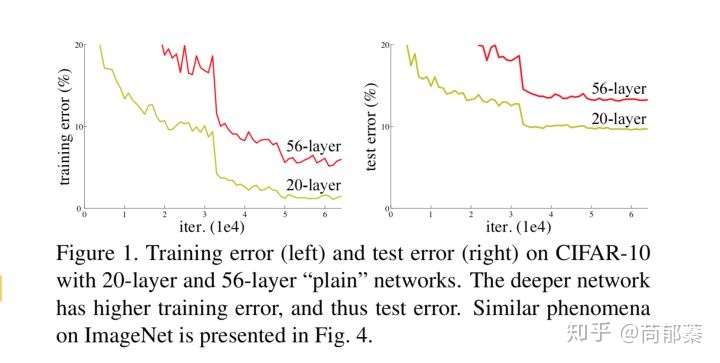img网络层数加深导致的训练问题

残差网络的定义

残差网络依旧让非线形层满足 [公式] ，然后从输入直接引入一个短连接到非线形层的输出上，使得整个映射变为

[公式]

这就是残差网路的核心公式，换句话说，残差是网络搭建的一种操作，任何使用了这种操作的网络都可以称之为残差网络。

一个具体的残差模块的定义如下图：

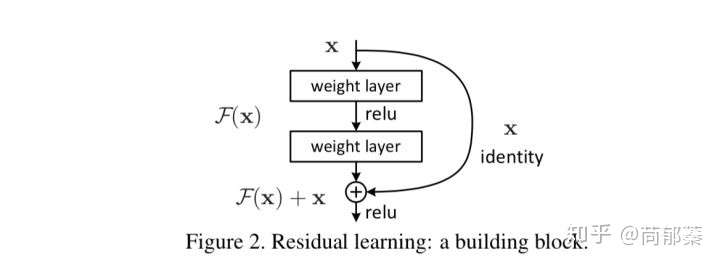img残差模块（由于先敲公式后引得图，容易混淆，图中的F(x)就是上文所说的H(x,w)，下面也一样替换）

残差网络的优势

残差模块为什么有效，有很多的解释，这里提供两个方面的理解，一方面是残差网络更好的拟合分类函数以获得更高的分类精度，另一方面是残差网络如何解决网络在层数加深时优化训练上的难题。

1.残差网络拟合函数的优越性

首先从万能近似定理（Universal Approximation Theorem）入手。这个定理表明，一个前馈神经网络（feedforward neural network）如果具有线性输出层，同时至少存在一层具有任何一种“挤压”性质的激活函数（例如logistic sigmoid激活函数）的隐藏层，那么只要给予这个网络足够数量的隐藏单元，它就可以以任意的精度来近似任何从一个有限维空间到另一个有限维空间的波莱尔可测函数(Borel Measurable Function)。

万能近似定理意味着我们在构建网络来学习什么函数的时候，我们知道一定存在一个多层感知机（Multilayer Perceptron Model，MLP）能够表示这个函数。然而，我们不能保证训练算法能够学得这个函数。因为即使多层感知机能够表示该函数，学习也可能会失败，可能的原因有两种。

（1）用于训练的优化算法可能找不到用于期望函数的参数值。

（2）训练算法可能由于过拟合而选择了错误的函数。

第二种过拟合情况不在我们的讨论范围之内，因此我们聚焦在前一种情况，为何残差网络相比简单的多层网络能更好的拟合分类函数，即找到期望函数的参数值。

对于普通的不带短连接的神经网络来说，存在这样一个命题。

命题1:假设 [公式] 为普通的带激活函数的全连接网络 [公式] 。 [公式] 为 [公式] 的正等值面，假如 [公式] 的每个层的激活函数都至多只有[公式] 个神经元，那么

[公式]

[公式] 为勒贝格测度。换句话说，这样狭窄的全连接网络表示的函数要么没有边界约束，要么恒为0。因此，即使层数无限加深，整个网络的表现力也受网络的宽度限制而无法近似一个带边界的区域。而对于残差网络来讲，拟合函数的能力则完全不受网路宽度的影响，上述命题1对于残差网络并不适用。

下面从一个简单的二维例子来说明这一点，这样可以进行方便的可视化。我们随机生成一组测试点 [公式] ，满足

[公式]

我们手动构造一个清晰的分类边界使得整个任务更容易一点，损失函数采用逻辑回归损失[公式] ，其中 [公式] 为网络对于样本 [公式] 的实际输出。经过训练后，分析网络不同深度下得到的训练边界，如图3.5可以发现宽度比输入维度小的残差网络的训练边界明显更加接近真实边界，也不受命题1的限制。

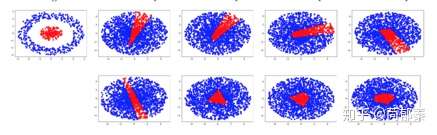img图3.5 不同网络结构拟合函数边界的结果。左上角为函数的真实边界。第一行是简单的全连接网络，每层的神经元个数为2；第二行为带短连接的网络，每层神经元个数为1。从左到右的网络层数依次递增，分别为1-5层。

事实上对于高维函数，这一特点依然适用。因此，当函数的输入维度非常高时，这一做法就变的非常有意义。尽管在高维空间这一特点很难被可视化，但是这个理论给了一个很合理的启发，就是原则上，带短连接的网络的拟合高维函数的能力比普通连接的网络更强。这部分我们讨论了残差网络有能力拟合更高维的函数，但是在实际的训练过程中仍然可能存在各种各样的问题使得学习到最优的参数非常困难，因此下一小节讨论残差在训练过程中的优越性。

2.残差网络训练过程的优越性

这个部分我们讨论为什么残差能够缓解深层网络的训练问题，以及探讨可能的短连接方式和我们最终选择的残差的理由。正如本章第三部分讨论的一样，整个残差卷积神经网络是由以上的残差卷积子模块堆积而成。如上一小节所定义的，假设第 [公式] 层的残差卷积字子模块的映射为

[公式]

[公式] 是第 [公式] 层的输入， [公式] 是第 [公式] 层的参数， [公式] 是残差单元层数。

那么第 [公式] 层的输入为

[公式]

因此得到

[公式]

循环带入这个式子 [公式] ，我们可以得到

[公式] （1）

对于任何深度的L来讲，上述式子（1）显示了一些良好的特性。

（1）第[公式]层的特征[公式]可以分为两个部分，第一部分是浅层的网络表示[公式]加上一个残差函数映射 [公式] ，表明模型在任意单元内都是一个残差的形式。

（2）对于任意深度 [公式] 的特征 [公式] 来讲，它是前面所有残差模块的和，这与简单的不加短连接的网络完全相反。原因是，不加短连接的网络在第 [公式] 层的特征 [公式] 是一系列的向量乘的结果，即 [公式] (在忽略batch normalization和激活函数的情况下)。

同样，上述式子显示有非常好的反向传播特性，假设损失为 [公式] ，根据链式求导法则，我们可以得到

[公式] （2）

显示梯度[公式]由两个部分组成，一部分 [公式] 是不用经过任何权重加权的信息流，另一部分是通过加权层的 [公式] ，两部分连接的线形特性保证了信息可以直接反向传播到浅层。同时式子还说明对于小的batch而言，梯度 [公式] 不太可能会消失，因为通常 对于小的batch来讲不会总是为1，那么这表示即使权重非常小，梯度也不会为0，不存在梯度消失的问题。

总之，式子（1）和（2）表明信号无论是在前向传播还是反向传播的过程中，都是可以直接通过的。

残差模块的实现例子

大家可以对照图看具体的实现：

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import torch.nn as nn
import torch
from torch.nn.init import kaiming_normal, constant

class BasicConvResBlock(nn.Module):

    def __init__(self, input_dim=128, n_filters=256, kernel_size=3, padding=1, stride=1, shortcut=False, downsample=None):
        super(BasicConvResBlock, self).__init__()

        self.downsample = downsample
        self.shortcut = shortcut

        self.conv1 = nn.Conv1d(input_dim, n_filters, kernel_size=kernel_size, padding=padding, stride=stride)
        self.bn1 = nn.BatchNorm1d(n_filters)
        self.relu = nn.ReLU()
        self.conv2 = nn.Conv1d(n_filters, n_filters, kernel_size=kernel_size, padding=padding, stride=stride)
        self.bn2 = nn.BatchNorm1d(n_filters)

    def forward(self, x):
        residual = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)

        if self.shortcut:
            out += residual

        out = self.relu(out)

        return out