一、K-Means(K均值)聚类

算法步骤：
(1) 首先我们选择一些类/组，并随机初始化它们各自的中心点。中心点是与每个数据点向量长度相同的位置。这需要我们提前预知类的数量(即中心点的数量)。
(2) 计算每个数据点到中心点的距离，数据点距离哪个中心点最近就划分到哪一类中。
(3) 计算每一类中中心点作为新的中心点。
(4) 重复以上步骤，直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点，然后选择运行结果最好的一个。
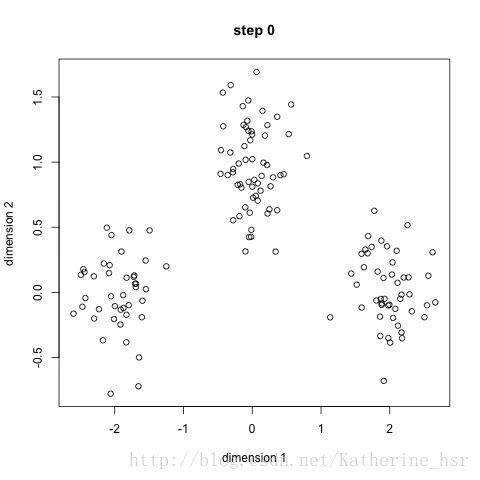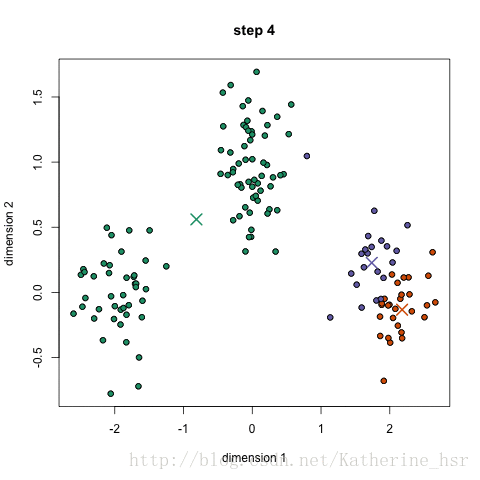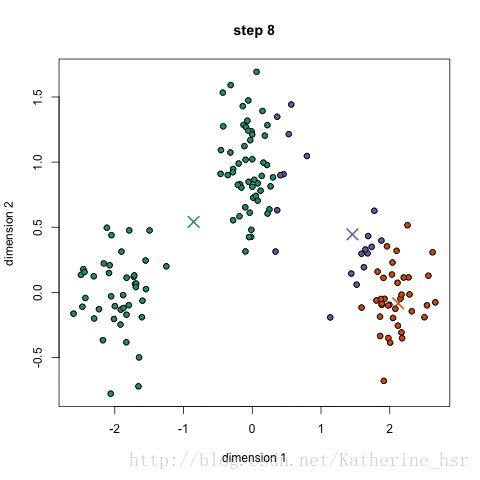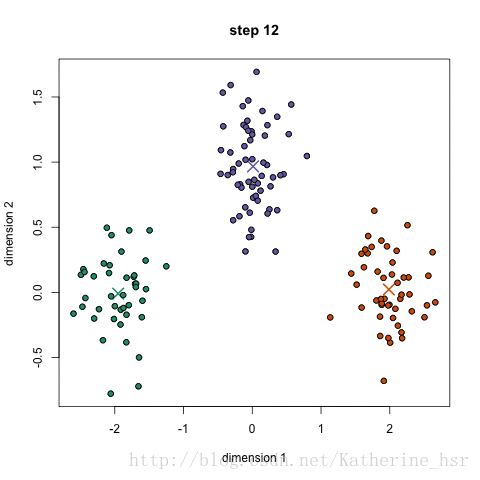
下图演示了K-Means进行分类的过程：

img

  • 优点
    • 速度快，计算简便
  • 缺点
    • 我们必须提前知道数据有多少类/组。

K-Medians是K-Means的一种变体，是用数据集的中位数而不是均值来计算数据的中心点。
K-Medians的优势是使用中位数来计算中心点不受异常值的影响；缺点是计算中位数时需要对数据集中的数据进行排序，速度相对于K-Means较慢。

KMeans 具体过程如下：

1、比如下面是随机的一些点，我们想将这些点分成三类，聚类中用簇（cluster）表示，那么离得比较近的点肯定归为一个簇，最理想的情况就是如下所示，不同簇用不同的颜色表示。

img

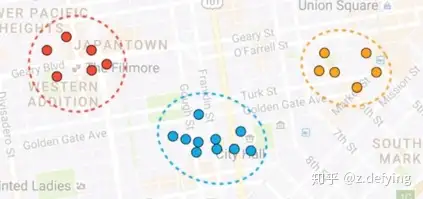
2、我们当然可以通过眼睛看来决定哪些点为一个簇，但是计算机不能，那么我们需要先进行初始化，即随机选三个点分别作为三个簇的中心，也就是质心，如下图的五角星。然后计算每个点到这三个质心的距离，将这些点分配给离它最近的质心。

img

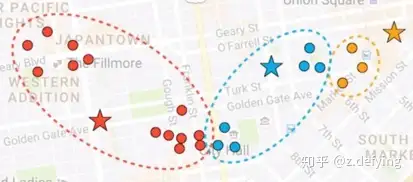
3、现在每个点都有所属的簇了，然后根据每个簇中的所有点重新计算簇的质心（一般是计算平均值），可以看到三个五角星的位置发生了变化。

img

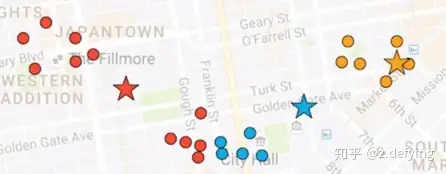
4、然后又计算每个点到三个新的质心的距离，又将这些点和离它最近的质心归为一类，这些点的所属类别就发生了变化。不断迭代这个过程，直到质心的位置基本不变。

最终的结果就可能如下图所示：

img

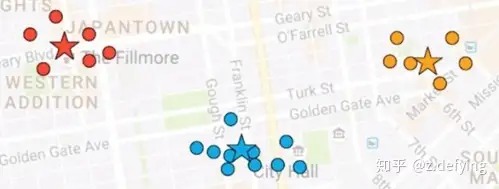
最刚开始的中心点是随机指定的，而中心点不同的指定方法，会使得聚类算法运行的最终结果有很大的不同。我们通常是进行多次初始化，多次运行聚类算法，取最好的那个结果。

KMeans 聚类算法有三个缺点：

  • 第一个就是对簇的数量的选择，我们希望指定一个簇数K，以使每个点和其最近的簇的距离之和最小。但是在实际情况中，我们很难找到一个合适的K值，因为我们不知道应该将数据分为几类。
  • Kmeans 算法会把所有的数据点都进行分类，但是很多情况下，会有一些离群点，这些点应该被剔除的，但是 Kmeans 算法还是会把它们归为某一类。
  • k均值聚类假设对每个簇来说，所有的方向都同等重要。这也就意味着k均值聚类主要适用于球形分布的数据，对于其他分布的数据分类可能不好。

机器学习漫谈

二、均值漂移聚类

均值漂移聚类是基于滑动窗口的算法，来找到数据点的密集区域。这是一个基于质心的算法，通过将中心点的候选点更新为滑动窗口内点的均值来完成，来定位每个组/类的中心点。然后对这些候选窗口进行相似窗口进行去除，最终形成中心点集及相应的分组。

具体步骤：

  1. 确定滑动窗口半径r，以随机选取的中心点C半径为r的圆形滑动窗口开始滑动。均值漂移类似一种爬山算法，在每一次迭代中向密度更高的区域移动，直到收敛。
  2. 每一次滑动到新的区域，计算滑动窗口内的均值来作为中心点，滑动窗口内的点的数量为窗口内的密度。在每一次移动中，窗口会想密度更高的区域移动。
  3. 移动窗口，计算窗口内的中心点以及窗口内的密度，知道没有方向在窗口内可以容纳更多的点，即一直移动到圆内密度不再增加为止。
  4. 步骤一到三会产生很多个滑动窗口，当多个滑动窗口重叠时，保留包含最多点的窗口，然后根据数据点所在的滑动窗口进行聚类。

下图演示了均值漂移聚类的计算步骤：

img

下面显示了所有滑动窗口从头到尾的整个过程。每个黑点代表滑动窗口的质心，每个灰点代表一个数据点。

img

  • 优点：
    • 不同于K-Means算法，均值漂移聚类算法不需要我们知道有多少类/组。
    • 基于密度的算法相比于K-Means受均值影响较小。
  • 缺点：
    • 窗口半径r的选择可能是不重要的。

三、基于密度的聚类方法(DBSCAN)

与均值漂移聚类类似，DBSCAN也是基于密度的聚类算法。
具体步骤：

  1. 首先确定半径r和minPoints. 从一个没有被访问过的任意数据点开始，以这个点为中心，r为半径的圆内包含的点的数量是否大于或等于minPoints，如果大于或等于minPoints则改点被标记为central point,反之则会被标记为noise point。
  2. 重复1的步骤，如果一个noise point存在于某个central point为半径的圆内，则这个点被标记为边缘点，反之仍为noise point。重复步骤1，知道所有的点都被访问过。
    • 优点：不需要知道簇的数量
    • 缺点：需要确定距离r和minPoints

四、用高斯混合模型（GMM）的最大期望（EM）聚类

K-Means的缺点在于对聚类中心均值的简单使用。下面的图中的两个圆如果使用K-Means则不能作出正确的类的判断。同样的，如果数据集中的点类似下图中曲线的情况也是不能正确分类的。

img

使用高斯混合模型（GMM）做聚类首先假设数据点是呈高斯分布的，相对应K-Means假设数据点是圆形的，高斯分布（椭圆形）给出了更多的可能性。我们有两个参数来描述簇的形状：均值和标准差。所以这些簇可以采取任何形状的椭圆形，因为在x，y方向上都有标准差。因此，每个高斯分布被分配给单个簇。
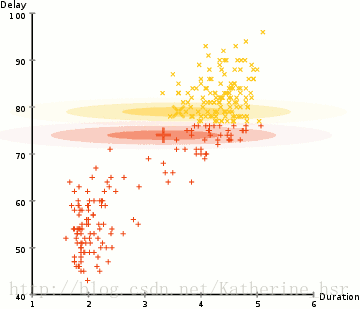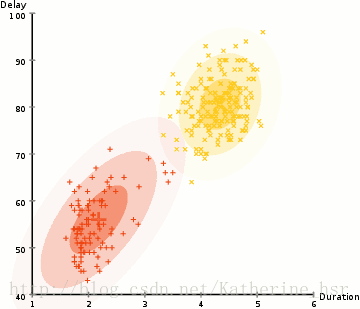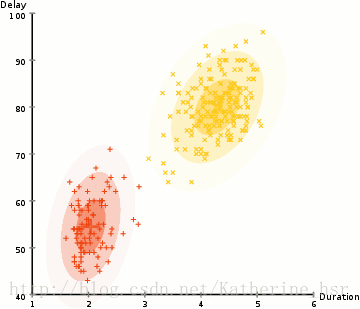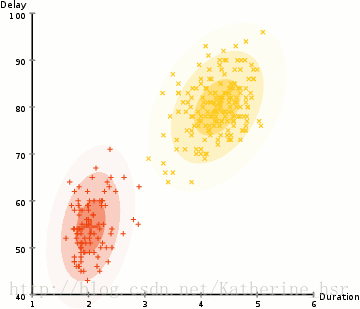
所以要做聚类首先应该找到数据集的均值和标准差，我们将采用一个叫做最大期望(EM)的优化算法。下图演示了使用GMMs进行最大期望的聚类过程。

img

具体步骤：

  1. 选择簇的数量（与K-Means类似）并随机初始化每个簇的高斯分布参数（均值和方差）。也可以先观察数据给出一个相对精确的均值和方差。
  2. 给定每个簇的高斯分布，计算每个数据点属于每个簇的概率。一个点越靠近高斯分布的中心就越可能属于该簇。
  3. 基于这些概率我们计算高斯分布参数使得数据点的概率最大化，可以使用数据点概率的加权来计算这些新的参数，权重就是数据点属于该簇的概率。
  4. 重复迭代2和3直到在迭代中的变化不大。
    GMMs的优点：（1）GMMs使用均值和标准差，簇可以呈现出椭圆形而不是仅仅限制于圆形。K-Means是GMMs的一个特殊情况，是方差在所有维度上都接近于0时簇就会呈现出圆形。
    （2）GMMs是使用概率，所有一个数据点可以属于多个簇。例如数据点X可以有百分之20的概率属于A簇，百分之80的概率属于B簇。也就是说GMMs可以支持混合资格。

五、凝聚层次聚类

层次聚类算法分为两类：自上而下和自下而上。凝聚层级聚类(HAC)是自下而上的一种聚类算法。HAC首先将每个数据点视为一个单一的簇，然后计算所有簇之间的距离来合并簇，知道所有的簇聚合成为一个簇为止。
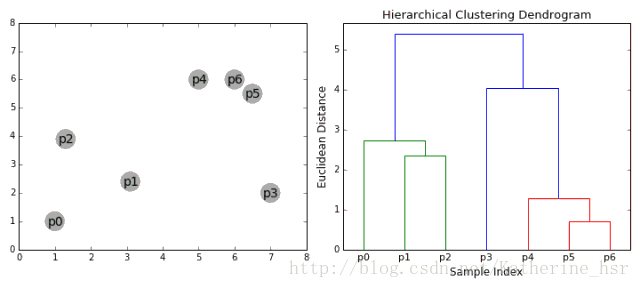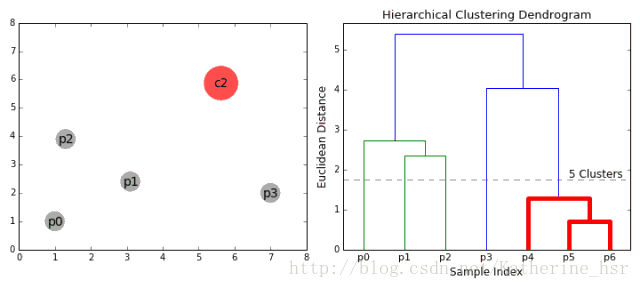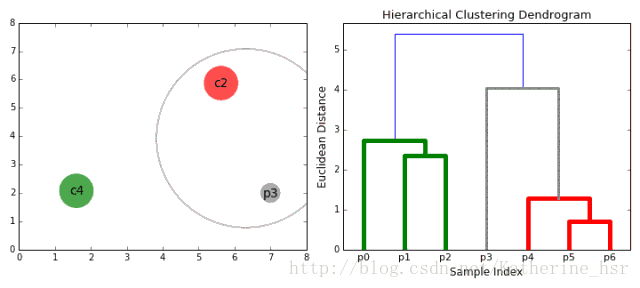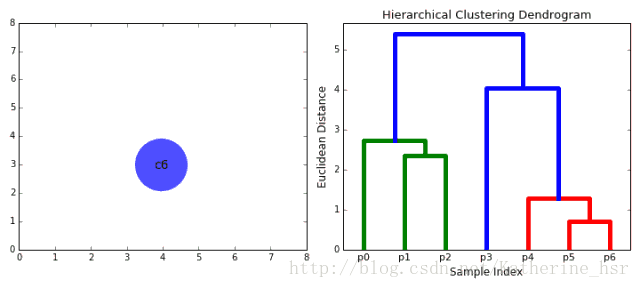
下图为凝聚层级聚类的一个实例：

img

具体步骤：

  1. 首先我们将每个数据点视为一个单一的簇，然后选择一个测量两个簇之间距离的度量标准。例如我们使用average linkage作为标准，它将两个簇之间的距离定义为第一个簇中的数据点与第二个簇中的数据点之间的平均距离。

  2. 在每次迭代中，我们将两个具有最小average linkage的簇合并成为一个簇。

  3. 重复步骤2知道所有的数据点合并成一个簇，然后选择我们需要多少个簇。

    层次聚类优点：

    （1）不需要知道有多少个簇
    （2）对于距离度量标准的选择并不敏感
    缺点：效率低

六、图团体检测(Graph Community Detection)

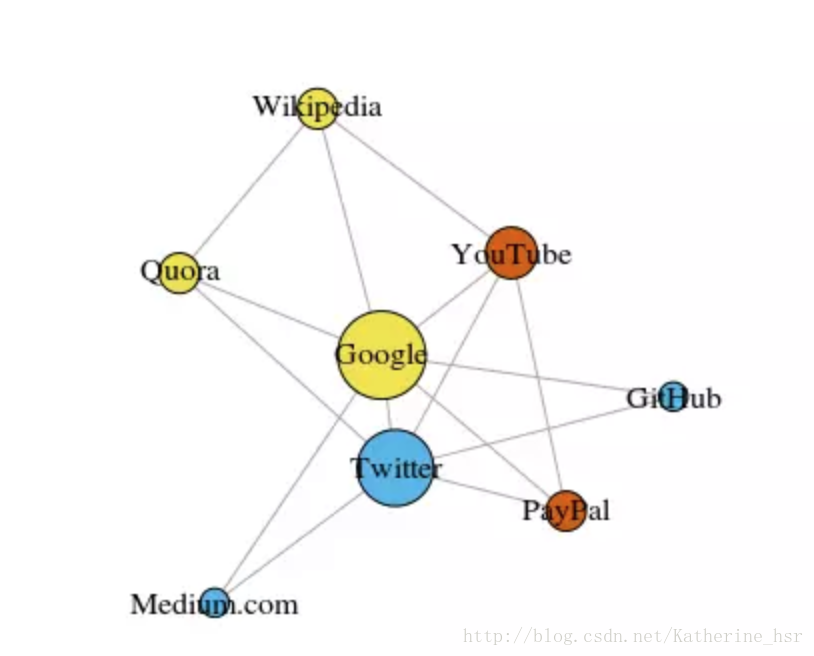
当我们的数据可以被表示为网络或图是，可以使用图团体检测方法完成聚类。在这个算法中图团体（graph community）通常被定义为一种顶点(vertice)的子集，其中的顶点相对于网络的其他部分要连接的更加紧密。下图展示了一个简单的图，展示了最近浏览过的8个网站，根据他们的维基百科页面中的链接进行了连接。

img

模块性可以使用以下公式进行计算：

组合学告诉我们对于一个仅有8个顶点的网络，就存在4140种不同的聚类方式，16个顶点的网络的聚类方式将超过100亿种。32个顶点的网络的可能聚类方式更是将超过10^21种。因此，我们必须寻找一种启发式的方法使其不需要尝试每一种可能性。这种方法叫做Fast-Greedy Modularity-Maximization(快速贪婪模块性最大化)的算法，这种算法在一定程度上类似于上面描述的集聚层次聚类算法。只是这种算法不根据距离来融合团体，而是根据模块性的改变来对团体进行融合。
具体步骤：

  1. 首先初始分配每个顶点到其自己的团体，然后计算整个网络的模块性 M。
  2. 第 1 步要求每个团体对（community pair）至少被一条单边链接，如果有两个团体融合到了一起，该算法就计算由此造成的模块性改变 ΔM。
  3. 第 2 步是取 ΔM 出现了最大增长的团体对，然后融合。然后为这个聚类计算新的模块性 M，并记录下来。
  4. 重复第 1 步和 第 2 步——每一次都融合团体对，这样最后得到 ΔM 的最大增益，然后记录新的聚类模式及其相应的模块性分数 M。
  5. 重复第 1 步和 第 2 步——每一次都融合团体对，这样最后得到 ΔM 的最大增益，然后记录新的聚类模式及其相应的模块性分数 M。

七、如何选择K值

如何选择K值

K-Means中K值的选择
（1）拍脑袋法
（2）肘部法则（Elbow Method）
（3）间隔统计量（Gap Statistic）
（4）轮廓系数（Silhouette Coefficient）
（5）Canopy算法
K-Means是一个很简单的聚类方法，说它简单，主要原因是使用它时只需设置一个K值（设置需要将数据聚成几类）。但问题是，有时候我们拿到的数据根本不知道要分为几类，对于二维的数据，我们还能通过肉眼观察法进行确定，超过二维的数据怎么办？今天就一起来学习下。

7.1 拍脑袋法

启发式算法，自己根据实际意义定K值。或者直接：

一个非常快速的，拍脑袋的方法是将样本量除以2再开方出来的值作为K值，具体公式为：
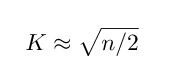
在这里插入图片描述

7.2 肘部法则（Elbow Method）

Elbow Method ：Elbow意思是手肘，如下图左所示，此种方法适用于 K 值相对较小的情况，当选择的k值小于真正的时，k每增加1，cost值就会大幅的减小；当选择的k值大于真正的K时， k每增加1，cost值的变化就不会那么明显。这样，正确的k值就会在这个转折点，类似elbow的地方。 如下图：

在这里插入图片描述

通过画K与cost function的关系曲线图，如左图所示，肘部的值(cost function开始时下降很快，在肘部开始平缓了)做为K值，K=3。并不是所有的问题都可以通过画肘部图来解决，有的问题如右边的那个图，肘点位置不明显（肘点可以是3，4，5），这时就无法确定K值了。故肘部图是可以尝试的一种方法，但是并不是对所有的问题都能画出如左边那么好的图来确定K值。

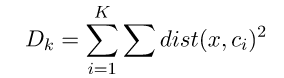
在这里插入图片描述

7.3 间隔统计量（Gap Statistic）

根据肘部法则选择最合适的K值有时并不是那么清晰，因此斯坦福大学的Robert等教授提出了Gap Statistic方法。
Gap Statistic的定义为:

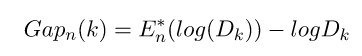
在这里插入图片描述

这里E(logDk)指的是logDk的期望。这个数值通常通过蒙特卡洛模拟产生，我们在样本里所在的矩形区域中（高维的话就是立方体区域）按照均匀分布随机地产生和原始样本数一样多的随机样本，并对这个随机样本做K-Means，从而得到一个Dk。如此往复多次，通常20次，我们可以得到20个log Dk。对这20个数值求平均值，就得到了E(logDk)的近似值。最终可以计算Gap Statisitc。而Gap statistic取得最大值所对应的K就是最佳的K。
Gap Statistic的基本思路是：引入参考的测值，这个参考值可以有Monte Carlo采样的方法获得。

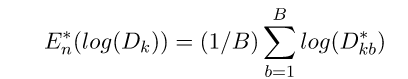
在这里插入图片描述

B是sampling的次数。为了修正MC带来的误差，我们计算sk也即标准差来矫正Gap Statistic。

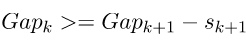
在这里插入图片描述

选择满足
在这里插入图片描述
的最小的k作为最优的聚类个数。下图阐释了Gap Statistic的过程。

在这里插入图片描述

在这里插入图片描述

7.4 轮廓系数法

Silhouette method 会衡量对象和所属簇之间的相似度——即内聚性（cohesion）。当把它与其他簇做比较，就称为分离性（separation）。该对比通过 silhouette 值来实现，后者在 [-1, 1] 范围内。Silhouette 值接近 1，说明对象与所属簇之间有密切联系；反之则接近 -1。若某模型中的一个数据簇，生成的基本是比较高的 silhouette 值，说明该模型是合适、可接受的。

方法：

1）计算样本i到同簇其他样本的平均距离a(i)。a(i)越小，说明样本i越应该被聚类到该簇。将a(i)称为样本i的簇内不相似度。簇C中所有样本的a(i)均值称为簇C的簇不相似度。

2）计算样本i到其他某簇C(j)的所有样本的平均距离b(ij)，称为样本i与簇C(j)的不相似度。定义为样本i的簇间不相似度：b(i) =min{bi1, bi2, …, bik}，b(i)越大，说明样本i越不属于其他簇。

3）根据样本i的簇内不相似度a i 和簇间不相似度b i ，定义样本i的轮廓系数：

在这里插入图片描述

4）判断：

s(i)接近1，则说明样本i聚类合理
s(i)接近-1，则说明样本i更应该分类到另外的簇
若s(i) 近似为0，则说明样本i在两个簇的边界上
所有样本的s(i )的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。但是，其缺陷是计算复杂度为O(n^2)，需要计算距离矩阵，那么当数据量上到百万，甚至千万级别时，计算开销会非常巨大。