10.31报告

参考自：R-CNN系列算法精讲：R-CNN —》Fast R-CNN —》Faster R-CNN 进阶之路

​ 深度学习——CNN(卷积神经网络)

​ 如何理解CNN中的感受野（receptive-field）？

​

一、进击的网络(CNN/DNN)

1.1 DNN与CNN区别（卷积神经网络）

img

上图为DNN深度神经网络图

DNN（(Deep Neural Networks，DNN）内部的神经网络层可以分为三类，输入层，隐藏层和输出层，一般来说第一层是输出层，最后一层是输出层，而中间的层数都是隐藏层。

img

上图为CNN神经网络

卷积神经网络（convolutional neural network, CNN），是一种专门用来处理具有类似网格结构的数据的神经网络。卷积网络是指那些至少在网络的一层中使用卷积运算来替代一般的矩阵乘法运算的神经网络。

总结：

（1）DNN是一种最简单的神经网络。各个神经元分别属于不同的层，每个神经元和前一层的所有神经元相连接，信号从输入层向输出层单向传播。

（2）CNN是一种通过卷积计算的前馈神经网络，其是受生物学上的感受野机制提出的，具有平移不变性，使用卷积核，最大的应用了局部信息，保留了平面结构信息。

（3）DNN以向量形式输入，未考虑平面的结构信息，而在图像领域和自然语言处理领域，平面信息很重要，因此CNN比DNN处理结果更好。由于DNN、CNN的输入、输出长度固定，而自然语言处理中的语句长度通常不固定，所以DNN、CNN处理这种问题效率较低，且无法处理时序相关的序列问题.为了解决这些问题，出现了循环神经网络RNN。

1
2
CNN给我的感觉就像滚雪球，不过这个雪球是反着滚的，把一个大的雪人（图片）通过均匀在道路（神经网络）上滚。
越滚越越远（网络越来越深）。最后滚成一个类别之类的东西也。

1.2 CNN的五种结构组成

1.2.1 输入层

​ 在处理图像的CNN中，输入层一般代表了一张图片的像素矩阵。可以用三维矩阵代表一张图片。三维矩阵的长和宽代表了图像的大小，而三维矩阵的深度代表了图像的色彩通道。比如黑白图片的深度为1，而在RGB色彩模式下，图像的深度为3。 类似这样一张64×64的jpg文件，本质上是3×64×64，三维矩阵。

1.2.2 卷积层(Convolution Layer)

​ **卷积层是CNN最重要的部分。**它与传统全连接层不同，卷积层中每一个节点的输入只是上一层神经网络的一小块。卷积层被称为过滤器(filter)或者内核(kernel)，Tensorflow的官方文档中称这个部分为过滤器(filter)。
【注意】在一个卷积层中，过滤器(filter)所处理的节点矩阵的长和宽都是由人工指定的，这个节点矩阵的尺寸也被称为过滤器尺寸。常用的尺寸有3x3或5x5，而过滤层处理的矩阵深度和当前处理的神经层网络节点矩阵的深度一致。

下图为卷积层过滤器(filter)结构示意图

img

下图为卷积过程

img

详细过程如下,Input矩阵是像素点矩阵，Kernel矩阵是过滤器(filter)

img

1.2.3 池化层(Pooling Layer)

​ 池化层不会改变三维矩阵的深度，但是它可以缩小矩阵的大小。通过池化层，可以进一步缩小最后全连接层中节点的个数，从而达到减少整个神经网络参数的目的。使用池化层既可以加快计算速度也可以防止过拟合。池化层filter的计算不是节点的加权和，而是采用最大值或者平均值计算。使用最大值操作的池化层被称之为最大池化层（max pooling）（最大池化层是使用的最多的磁化层结构）。使用平均值操作的池化层被称之为平均池化层（mean pooling）。

下图分别表示不重叠的4个2x2区域的最大池化层（max pooling）、平均池化层（mean pooling）。

img img

1.2.4 全连接层**（fully connected layers，FC)**

​ 在经过多轮卷积层和池化层的处理之后，在CNN的最后一般会由1到2个全连接层来给出最后的分类结果。经过几轮卷积层和池化层的处理之后，可以认为图像中的信息已经被抽象成了信息含量更高的特征。我们可以将卷积层和池化层看成自动图像特征提取的过程。在提取完成之后，仍然需要使用全连接层来完成分类任务。

​ 全连接层（fully connected layers，FC）在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中，全连接层可由卷积操作实现：对前层是全连接的全连接层可以转化为卷积核为1x1的卷积；而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积，h和w分别为前层卷积结果的高和宽。

​ 全连接层的作用主要就是实现分类（Classification）。

​ 全连接的核心操作就是矩阵向量乘积。

img

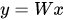
​ 本质就是由一个特征空间线性变换到另一个特征空间。目标空间的任一维——也就是隐层的一个 cell——都认为会受到源空间的每一维的影响。不考虑严谨，可以说，目标向量是源向量的加权和。

​ 在 CNN 中，全连接常出现在最后几层，用于对前面设计的特征做加权和。比如 mnist，前面的卷积和池化相当于做特征工程，后面的全连接相当于做特征加权。（卷积相当于全连接的有意弱化，按照局部视野的启发，把局部之外的弱影响直接抹为零影响；还做了一点强制，不同的局部所使用的参数居然一致。弱化使参数变少，节省计算量，又专攻局部不贪多求全；强制进一步减少参数。少即是多） 在 RNN 中，全连接用来把 embedding 空间拉到隐层空间，把隐层空间转回 label 空间等。

1
2
3
4
5
6
7
8
9
理解1：
   卷积取的是局部特征，全连接就是把以前的局部特征重新通过权值矩阵组装成完整的图。
因为用到了所有的局部特征，所以叫全连接。
理解2：
   从卷积网络谈起，卷积网络在形式上有一点点像咱们正在召开的“人民代表大会制度”。卷积核的个数相当于候选人，图像中不同的特征会激活不同的“候选人”（卷积核）。
池化层（仅指最大池化）起着类似于“合票”的作用，不同特征在对不同的“候选人”有着各自的喜好。
   全连接相当于是“代表普选”。所有被各个区域选出的代表，对最终结果进行“投票”，全连接保证了receiptive field 是整个图像，既图像中各个部分（所谓所有代表），都有对最终结果影响的权利。
理解3：
   假设你是一只小蚂蚁，你的任务是找小面包。你的视野还比较窄，只能看到很小一片区域。当你找到一片小面包之后，你不知道你找到的是不是全部的小面包，所以你们全部的蚂蚁开了个会，把所有的小面包都拿出来分享了。全连接层就是这个蚂蚁大会~

1.2.5 Softmax层(归一化指数函数)

​ 通过Softmax层，可以得到当前样例属于不同种类的概率分布问题。

​ 它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来。下图展示了softmax的计算方法：

img

​ 二分类就用sigmoid转化到 0~1 。

1.2.5 感受野（receptive field，RF）

感受野指的是一个特定的CNN特征（特征图上的某个点）在输入空间所受影响的区域。一个感受野可以用中心位置(center location)和大小(size)来表征。然而，对于一个CNN特征来说，感受野中的每个像素值（pixel）并不是同等重要。一个像素点越接近感受野中心，它对输出特征的计算所起作用越大。这意味着某一个特征不仅仅是受限在输入图片中某个特定的区域（感受野），并且呈指数级聚焦在区域的中心。这个重要的发现会在下一篇文章中讲。现在，我们关注如何计算一个特定感受野的中心位置和大小。

在CNN中，感受野应该是一个很重要的东西，但是往往被大家忽略，在我看到的文献中，图像分割模型DeepLab就提到了感受野大小的问题，但是那里并没有给出计算公式，如果采用上面的公式就可以快速得到结果。对于图像分割，感受野大小对分割效果是有很大影响的，所以DeepLab采用了扩展卷积（Atrous Convolution， Dilated Convolution）来增加感受野大小。对于空洞卷积来说，你可以将其转化为普通卷积（卷积核大小增加）来计算特征图的感受野。另外，上面的公式同样适用于池化层，因为其在结构上与卷积层是类似的。

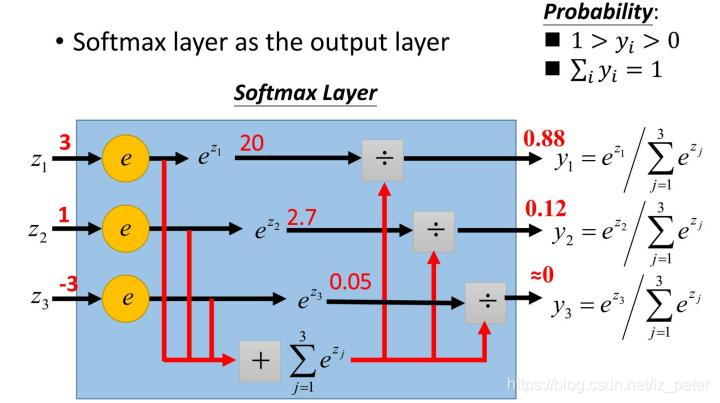
图1为给出了某些感受野实例。其中输入特征图大小为 [公式] ，采用的卷积参数如下：卷积核大小 [公式] ，padding大小 [公式] ，步长 [公式] 。经过一次卷积之后，得到大小为 [公式] 的输出特征图（绿色）。在这个特征图上继续采用相同的卷积，得到一个 [公式] 的特征图（橙色）。输出特征图的大小可以通过如下公式计算（参考A guide to convolution arithmetic for deep learning）：

img

为了简化讲解，这里假定CNN架构是对称的，并且输入图片是方形的。因此所有的卷积层的所有参数在两个维度上都是相同的。如果CNN架构或者输入图片是非对称的，你可以为各个维度单独计算特征图的属性。

img

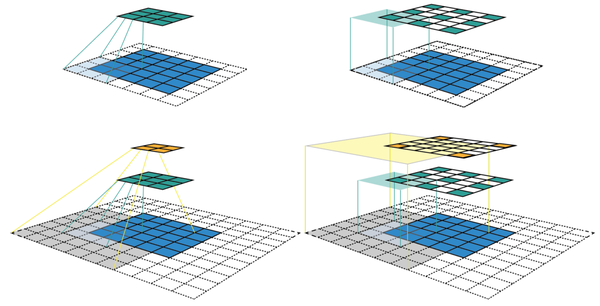
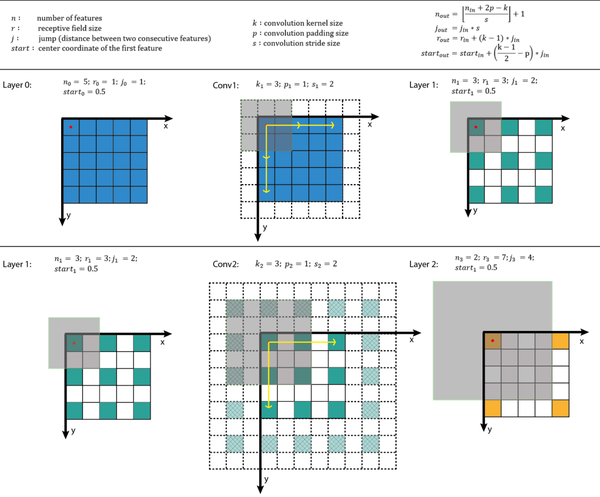
图1 CNN特征图的两种可视化方法

图1的左栏给出了CNN特征图可视化最常用的方式。在这个可视化中，我们可以看到每个特征图所包含的特征数，但是很难知道每个特征的感受野的中心位置和大小，对于深度CNN，我们没有办法追踪到感受野信息。右栏给出的是固定大小的CNN可视化，所有的特征图固定大小并保持与输入特征图大小一致，这可以解决前面的问题。每个特征被标记在其感受野所在的中心（从而定位出感受野中心位置）。由于一个特征图中所有的特征都有相同大小的感受野，我们可以简单地在每个特征周围画出一个边界框，从而获得感受野的大小。我们也没有必要将这个边界框向下映射到输入层，因为特征图已经与输入层具有相同的大小。图2给出了另外一个实例，其中输入特征图更大，为 [公式] ，与前面例子采用相同的卷积。图的左栏和右栏分别给出了固定大小CNN特征图的3D和2D可视化。可以看出感受野大小增加迅速，以至于第二个特征层的中心特征的感受野已经覆盖了整个输入特征图。这在深度CNN中是一个很重要的设计理念以提升性能。

img

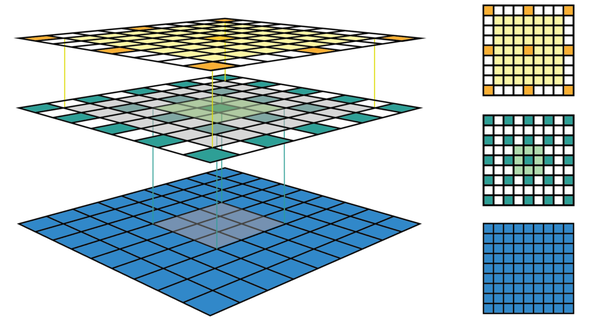
感受野计算公式

为了计算CNN每一层的感受野，除了要知道特征图每个维度的特征数 [公式]，还需要记录每一层的其他信息，这包括当前层的感受野大小 [公式] ，两个相邻特征的距离（跳跃的距离，如前面可视化所示） [公式] ，和左上角特征（第一个特征）的中心坐标 [公式] 。注意感受野（其实是特征图第一个特征的感受野）的中心坐标就等于这个特征的中心坐标，就如前面可视化中所示。当采用的卷积其核大小为 [公式] ，padding大小为 [公式] ，步长为 [公式] ，输出特征图的感受野可以按照如下公式计算：

img

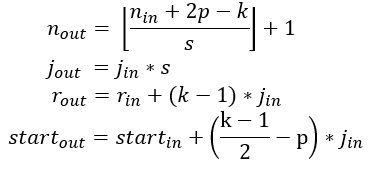
  • 第一个式子根据输入特征图大小以及卷积参数计算输出特征图大小，前面已经说过。
  • 第二个式子计算输出特征图的特征间的间隔 [公式] ，其等于上一层的间隔值乘以卷积的步长，所以间隔值将是按照步长呈指数级增长。
  • 第三个式子计算输出特征图的感受野大小，其等于前一层感受野大小加上 [公式] ，所以感受野是呈指数级增加，并且还有一个因子 [公式] 。
  • 第四个式子计算输出特征图的第一个特征感受野的中心坐标，其等于第一层的中心坐标加上 [公式] ，再减去 [公式] ，注意两项都要乘以前一层的间隔距离以得到实际距离。

对于第一层，一般是输入图片，其各项值为： [公式] 。图3给出了一个如何计算感受野的实例，图中的坐标系统中，输入层的第一个特征中心位置记为 [公式] 。通过利用上面公式迭代地进行计算，你可以计算出CNN中所有特征图的感受野信息。

img

1.3.其他参数

1.3.1 Dropout

dropout 是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。

主要要来减少过拟合。

该论文从神经网络的难题出发，一步一步引出dropout为何有效的解释。大规模的神经网络有两个缺点：

  • 费时
  • 容易过拟合

​ 这两个缺点真是抱在深度学习大腿上的两个大包袱，一左一右，相得益彰，额不，臭气相投。过拟合是很多机器学习的通病，过拟合了，得到的模型基本就废了。而为了解决过拟合问题，一般会采用ensemble方法，即训练多个模型做组合，此时，费时就成为一个大问题，不仅训练起来费时，测试起来多个模型也很费时。总之，几乎形成了一个死锁。

​ Dropout的出现很好的可以解决这个问题，每次做完dropout，相当于从原始的网络中找到一个更瘦的网络，如下图所示：

img

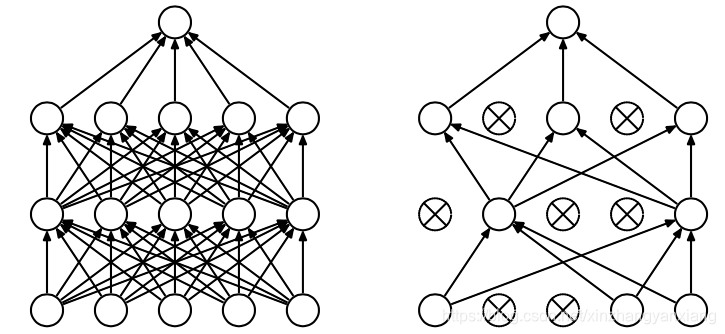
​ 因而，对于一个有N个节点的神经网络，有了dropout后，就可以看做是2n个模型的集合了，但此时要训练的参数数目却是不变的，这就解脱了费时的问题。

1.3.2 激活函数

​ 激活函数用来增加非线性因素的，提高模型拟合能力。如果不存在激活函数，神经网络的每一层的输入都是对前面输入的线性变化，就算把网络加到很深也无法去拟合任意函数的。

详情请见：激活函数

1.3.3 损失函数

​ 损失函数loss function）是用来估量模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。

详情请见：损失函数

1.3.4 padding

在卷积操作之前填充这幅图像。

在这个案例中，你可以沿着图像边缘再填充一层像素。如果你这样操作了，那么6×6的图像就被你填充成了一个8×8的图像。如果你用3×3的图像对这个8×8的图像卷积，你得到的输出就不是4×4的，而是6×6的图像，你就得到了一个尺寸和原始图像6×6的图像。习惯上，你可以用0去填充，如果是填充的数量，在这个案例中，，因为我们在周围都填充了一个像素点，输出也就变成了，所以就变成了，和输入的图像一样大。这个涂绿的像素点（左边矩阵）影响了输出中的这些格子（右边矩阵）。这样一来，角落或图像边缘的信息发挥的作用较小的这一缺点就被削弱了。

img

刚才已经展示过用一个像素点来填充边缘，如果你想的话，也可以填充两个像素点，也就是说在这里填充一层。实际上你还可以填充更多像素。我这里画的这种情况，填充后p = 2。

img
Valid卷积：

Valid卷积意味着不填充。

Same卷积

Same卷积意味你填充后，你的输出大小和输入大小是一样的。

为了指定卷积操作中的padding，你可以指定p的值。也可以使用Valid卷积，也就是p = 0。也可使用Same卷积填充像素，使你的输出和输入大小相同。

二、目标检测的敲门砖（R-CNN）

2.1 历史背景

img

​ 我们常说的R-CNN系列，一共包含三个版本：R-CNN、Fast R-CNN、Faster R-CNN。从命名上看，R是Region的缩写，CNN指我们常说的卷积神经网络。那么R-CNN其实就是使用推荐区域的卷积神经网络。由Fast、Faster很容易知道，版本的更迭解决的是一个实时性的问题。

​ R-CNN算法最早在2013年被提出，它的出现打开了运用深度学习进行目标检测的大门，从此之后，目标检测的精准度与实时性被不断刷新。R-CNN系列算法自提出之际，就非常引人注目，以至于在之后的很多经典算法中，如SSD、YOLO系列、Mask R-CNN中都能看到它的影子。

​ 学习R-CNN系列算法不仅能够让我们了解到基础的目标检测算法的思路，而且能够让学习者更加轻松地掌握SSD、YOLO系列、Mask R-CNN等算法。因为相比一些one-stage 的目标检测算法，Faster R-CNN作为two-stage的算法理解起来并不算简单。正是如此，当我们掌握了R-CNN系列算法后，再去学习经典的one-stage算法，就会变得异常简单。

​ R-CNN、Fast R-CNN采用的还是传统的SS算法生成推荐区域，计算非常耗时，达不到实时检测的效果。直到Faster R-CNN才使用RPN代替了原来的SS算法，才使得目标检测的时间大大缩短，达到实时性的效果。因此，本篇博客先会对R-CNN、Fast R-CNN进行一个简明扼要地讲解，大家只需了解算法的思路和演进过程即可；之后，会着重讲解R-CNN 系列的灵魂之作——Faster R-CNN，而这部分才是大家需要着重了解的。

​ 2013年11月，Ross Girshick等人最早提出了R-CNN算法，打开了利用深度学习进行目标检测的大门。在当时来说，R-CNN算法的目标检测水平超群，比传统的目标检测方法有了很大提升。实验表明，R-CNN算法在PASCAL VOC数据集取得了很好的成绩，这种算法的平均精确度比之前在VOC2012数据集上的最好测试效果还要高30%。并且，由该算法提出的论文《Rich feature hierarchies for accurate object detection and semantic segmentation》获得了世界计算机视觉顶会CVPR2014的最佳论文奖。

2.2 R-CNN

img

如上图所示，R-CNN目标检测算法流程主要分四个步骤：

  1. 采用SS(Selective Search)方法，使一张图片生成1000~2000个候选区域(region proposals)。
  2. 对每一个候选区域，都使用深度神经网络（AlexNet）提取特征，得到1*4096的特征向量。
  3. 将每一个特征向量送入每一类的SVM分类器，判断是否属于该类。
  4. 对已分类的推荐框进行线性回归，对这些框进行精细地调整，得到更加准确的边界框坐标。

R-CNN算法的检测效果很好，但是检测速度很慢，因此总体效率不高。其主要原因在于：

  • 提取特征操作非常冗余。检测时，需要将每个推荐区域都送入训练好的模型（AlexNet）进行前向传播，因此每张图片大约要进行1000~2000次前向传播。
  • 训练速度慢，过程繁琐。要单独分别训练三个不同的模型：CNN用来提取图像特征、SVM分类器用来预测类别、回归器精细修正建议框的位置。分开训练，耗时耗力。
  • 使用Selective Search算法生成推荐区域，这个过程大约耗时2s，也是它不能达到实时性检测的一个重要原因。

2.3 Fast-R-CNN

Fast R-CNN紧随R-CNN其后。Fast R-CNN更快更好，得益于以下几点:

  • 在提出区域之前先对图像进行特征提取，这样整个图像上只运行一个CNN，而不是2000个CNN的2000多个重叠区域
  • 将支持向量机替换为softmax层，从而扩展用于预测的神经网络，而不是创建新的模型

从直觉上看，移除2000个conv层，而只使用一次Convolution，并在其上创建方框是很有意义的。

2.4 Faster R-CNN

Fast R-CNN的缺点之一是缓慢的选择搜索算法，而Faster R-CNN引入了一种叫做网络和区域候选网络(RPN)的东西。

RPN工作原理：

在初始CNN的最后一层，一个3x3滑动窗口在feature map上移动，并将其映射到一个较低的维度(例如256-d)。对于每个滑动窗口位置，它基于k个固定比例锚框(默认边界框)生成多个可能的区域。

每个推荐区域包含以下内容：

  • 该区域的“客观性”得分
  • 4个表示区域边界框的坐标

换句话说，我们查看上一个区域中的每个位置，并考虑k个围绕它的不同框:一个高框，一个宽框，一个大框，等等。对于每个方框，我们输出它是否包含对象，以及方框的坐标是什么。这是为什么看着像个一个滑动窗口位置:

2k分数表示每个k边界框在“对象”上的softmax概率。注意，尽管RPN输出边界框坐标，但它并不试图分类任何潜在的对象:它的唯一工作仍然是提出对象区域。如果锚框的“客观性”得分高于某个阈值，则该框的坐标将作为区域建议向前传递。

一旦我们有了我们的区域提案，我们就直接把它们输入到本质上是fast R-CNN。我们添加了一个池化层，一些完全连接层，最后一个softmax分类层和边界框回归器。在某种意义上，Faster R-CNN = RPN + Fast R-CNN.