LR逻辑回归(logistics regression)

逻辑回归是一个分类算法，它可以处理二元分类以及多元分类。
逻辑回归就是根据之前的数据，预测某事件为真的概率值

一.分类和回归任务的区别

我们可以按照任务的种类,将任务分为回归任务和分类任务.那这两者的区别是什么呢?按照较官方些的说法,输入变量与输出变量均为连续变量的预测问题是回归问题,输出变量为有限个离散变量的预测问题成为分类问题.

通俗一点讲,我们要预测的结果是一个数,比如要通过一个人的饮食预测一个人的体重,体重的值可以有无限多个,有的人50kg,有的人51kg,在50和51之间也有无限多个数.这种预测结果是某一个确定数,而具体是哪个数有无限多种可能的问题,我们会训练出一个模型,传入参数后得到这个确定的数,这类问题我们称为回归问题.预测的这个变量(体重)因为有无限多种可能,在数轴上是连续的,所以我们称这种变量为连续变量.
我们要预测一个人身体健康或者不健康,预测会得癌症或者不会得癌症,预测他是水瓶座,天蝎座还是射手座,这种结果只有几个值或者多个值的问题,我们可以把每个值都当做一类,预测对象到底属于哪一类.这样的问题称为分类问题.如果一个分类问题的结果只有两个,比如"是"和"不是"两个结果,我们把结果为"是"的样例数据称为"正例",讲结果为"不是"的样例数据称为"负例",对应的,这种结果的变量称为离散型变量.

二.逻辑回归不是回归

从名字来理解逻辑回归.在逻辑回归中,逻辑一词是logistics [lə’dʒɪstɪks]的音译字,并不是因为这个算法是突出逻辑的特性.

至于回归,我们前一段讲到回归任务是结果为连续型变量的任务,logistics regression是用来做分类任务的,为什么叫回归呢?那我们是不是可以假设,逻辑回归就是用回归的办法来做分类的呢.跟上思路.

三.怎么做

假设刚刚的思路是正确的,逻辑回归就是在用回归的办法做分类任务,那有什么办法可以做到呢,此时我们就先考虑最简单的二分类,结果是正例或者负例的任务.

按照多元线性回归的思路,我们可以先对这个任务进行线性回归,学习出这个事情结果的规律,比如根据人的饮食,作息,工作和生存环境等条件预测一个人"有"或者"没有"得恶性肿瘤,可以先通过回归任务来预测人体内肿瘤的大小,取一个平均值作为阈值,假如平均值为y,肿瘤大小超过y为恶心肿瘤,无肿瘤或大小小于y的,为非恶性.这样通过线性回归加设定阈值的办法,就可以完成一个简单的二分类任务.如下图:

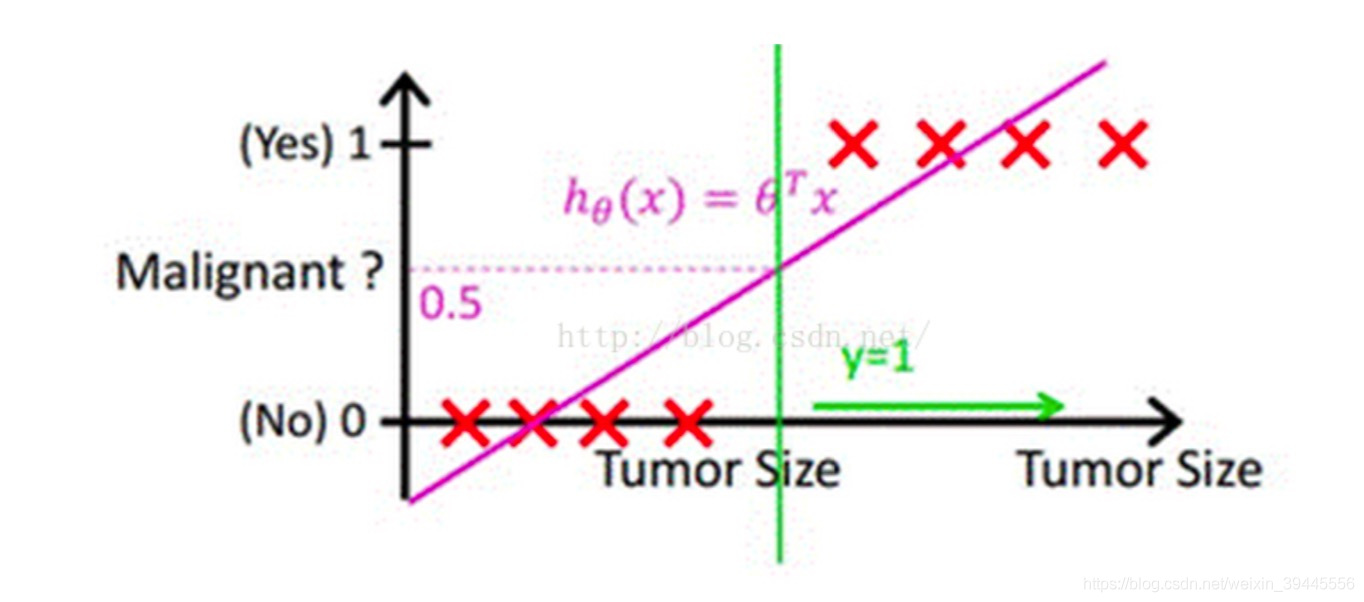
上图中,红色的x轴为肿瘤大小,粉色的线为回归出的函数的图像,绿色的线为阈值.
预测肿瘤大小还是一个回归问题,得到的结果(肿瘤的大小)也是一个连续型变量.通过设定阈值,就成功将回归问题转化为了分类问题.但是,这样做还存在一个问题.

我们上面的假设,依赖于所有的肿瘤大小都不会特别离谱,如果有一个超大的肿瘤在我们的例子中,阈值就很难设定.加入还是取平均大小为阈值,则会出现下图的情况:

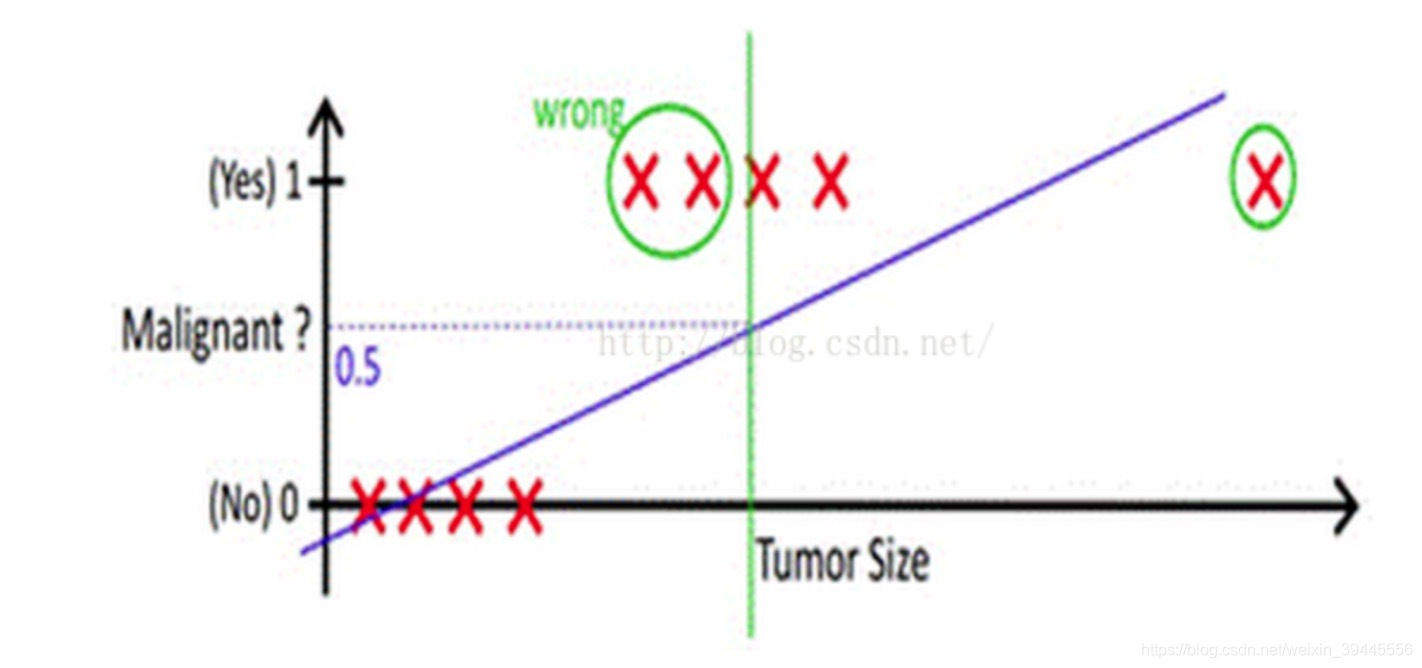
从上边的例子可以看出,使用线性的函数来拟合规律后取阈值的办法是行不通的,行不通的原因在于拟合的函数太直,离群值(也叫异常值)对结果的影响过大,但是我们的整体思路是没有错的,错的是用了太"直"的拟合函数,如果我们用来拟合的函数是非线性的,不这么直,是不是就好一些呢?

所以我们下面来做两件事:

1 2	1-找到一个办法解决掉回归的函数严重受离群值影响的办法. 2-选定一个阈值.

四:把回归函数掰弯

没错,本小节用来解决上边说的第一个问题.开玩笑了,无论如何我也不可能掰弯这个函数.我们能做的呢,就是换一个.原来的判别函数我们用线性的y = $w^{T}x$ ,逻辑回归的函数呢,我们目前就用sigmod函数,函数如下:

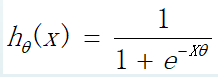
公式中,e为欧拉常数(是常数,如果不知道,自行百度),Z就是我们熟悉的多元线性回归中的 $W^{T}X$ ,建议现阶段大家先记住逻辑回归的判别函数用它就好了.

就像我们说多元线性回归的判别函数为 $y = w_{0}x_{0} + w_{1}x_{1} + ... +w_{n}x_{n}$ 一样.追究为什么是他花费的经历会比算法本身更多.

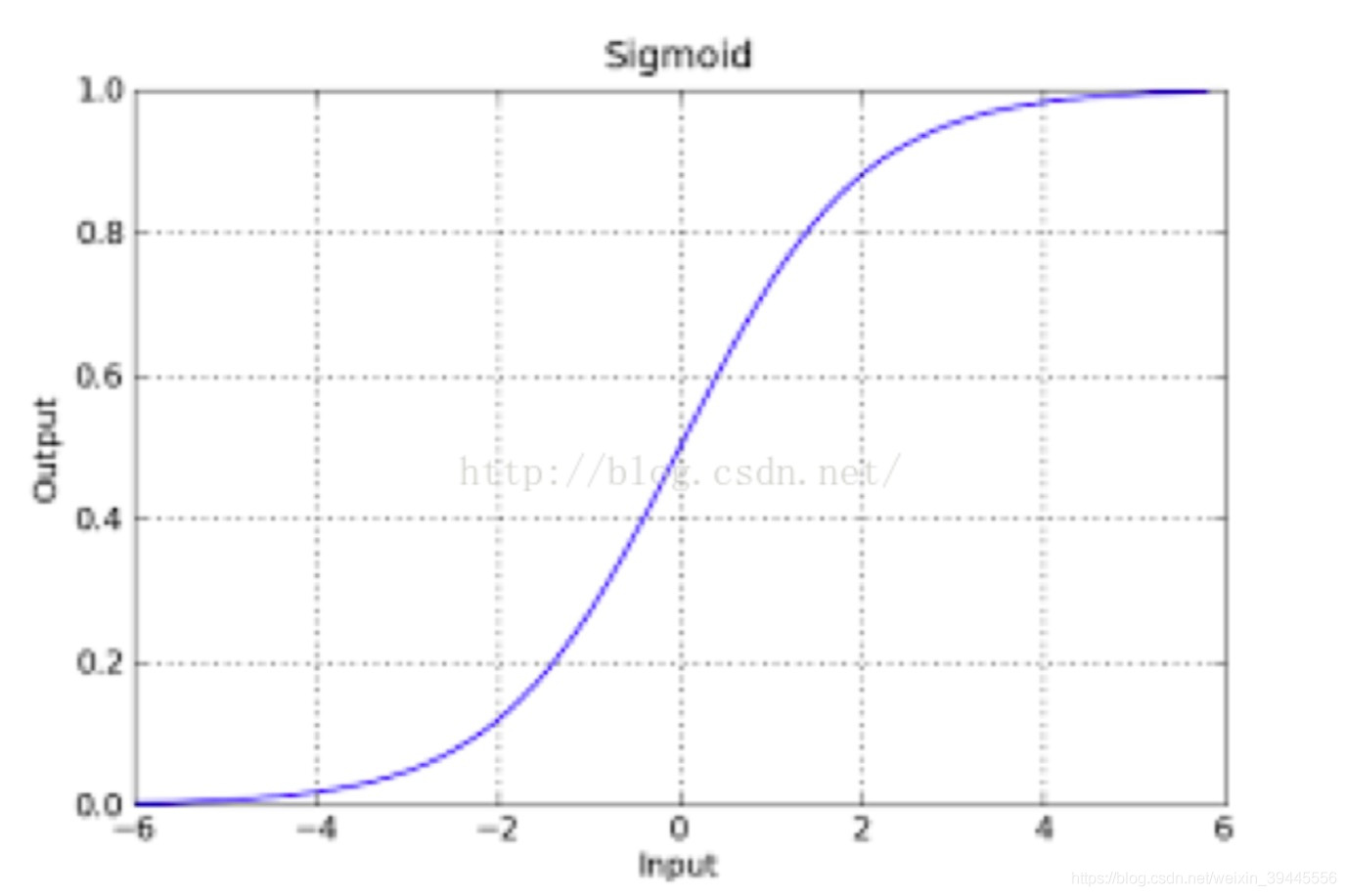
sigmod函数的图像如下:

1 2	z = numpy.dot(X, theta) #python代码 h = 1/(1+numpy.exp(-z)) # exp: e 的多少次方

该函数具有很强的鲁棒性(鲁棒是Robust的音译，也就是健壮和强壮的意思),并且将函数的输入范围(∞,-∞)映射到了输出的(0,1)之间且具有概率意义.具有概率意义是怎么理解呢:将一个样本输入到我们学习到的函数中,输出0.7,意思就是这个样本有70%的概率是正例,1-70%就是30%的概率为负例.

再次强调一下,如果你的数学功底很好,可以看一下我上边分享的为什么是sigmod函数的连接,如果数学一般,我们这个时候没有必要纠结为什么是sigmod,函数那么多为什么选他.学习到后边你自然就理解了

总结一下上边所讲:我们利用线性回归的办法来拟合然后设置阈值的办法容易受到离群值的影响,sigmod函数可以有效的帮助我们解决这一个问题,所以我们只要在拟合的时候把即y = $y = w_{0}x_{0} + w_{1}x_{1} + ... +w_{n}x_{n}$ 换成 $W^{T}X$ 即可,其中

z= $W^{T}X$ ,也就是说g(z) = $\frac{1}{1 + e^{w^{T}x}}$ . 同时,因为g(z)函数的特性,它输出的结果也不再是预测结果,而是一个值预测为正例的概率,预测为负例的概率就是1-g(z).

函数形式表达:

         P(y=0|w,x) = 1 – g(z)

         P(y=1|w,x) =  g(z)

         P(正确) = *         为某一条样本的预测值,取值范围为0或者1.

到这里,我们得到一个回归函数,它不再像y=wT * x一样受离群值影响,他的输出结果是样本预测为正例的概率(0到1之间的小数).我们接下来解决第二个问题:选定一个阈值.

五:选定阈值

选定阈值的意思就是,当我选阈值为0.5,那么小于0.5的一定是负例,哪怕他是0.49.此时我们判断一个样本为负例一定是准确的吗?其实不一定,因为它还是有49%的概率为正利的.但是即便他是正例的概率为0.1,我们随机选择1w个样本来做预测,还是会有接近100个预测它是负例结果它实际是正例的误差.无论怎么选,误差都是存在的.所以我们选定阈值的时候就是在选择可以接受误差的程度.
我们现在知道了sigmod函数预测结果为一个0到1之间的小数,选定阈值的第一反应,大多都是选0.5,其实实际工作中并不一定是0.5,阈值的设定往往是根据实际情况来判断的.本小节我们只举例让大家理解为什么不完全是0.5,并不会有一个万能的答案,都是根据实际工作情况来定的.

0到1之间的数阈值选作0.5当然是看着最舒服的,可是假设此时我们的业务是像前边的例子一样,做一个肿瘤的良性恶性判断.选定阈值为0.5就意味着,如果一个患者得恶性肿瘤的概率为0.49,模型依旧认为他没有患恶性肿瘤,结果就是造成了严重的医疗事故.此类情况我们应该将阈值设置的小一些.阈值设置的小,加入0.3,一个人患恶性肿瘤的概率超过0.3我们的算法就会报警,造成的结果就是这个人做一个全面检查,比起医疗事故来讲,显然这个更容易接受.
第二种情况,加入我们用来识别验证码,输出的概率为这个验证码识别正确的概率.此时我们大可以将概率设置的高一些.因为即便识别错了又能如何,造成的结果就是在一个session时间段内重试一次.机器识别验证码就是一个不断尝试的过程,错误率本身就很高.

以上两个例子可能不大准确,只做意会,你懂了就好.

	到这里,逻辑回归的由来我们就基本理清楚了,现在我们知道了逻辑回归的判别函数就是![img](https://private.codecogs.com/gif.latex?g%28z%29%20%3D%20%5Cfrac%7B1%7D%7B1+e%5E%7B-z%7D%7D)

，z= $W^{T}X$

六.最大似然估计

此时我们想要找到一组w,使函数 $g(z) = \frac{1}{1+e^{-z}}$ 正确的概率最大.而我们在上面的推理过程中已经得到每个单条样本预测正确概率的公式:

	P(正确) =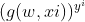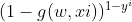![(g(w,xi))^{y^{i}}](https://private.codecogs.com/gif.latex?%28g%28w%2Cxi%29%29%5E%7By%5E%7Bi%7D%7D) *![img](https://private.codecogs.com/gif.latex?%281-g%28w%2Cxi%29%29%5E%7B1-y%5E%7Bi%7D%7D)

	若想让预测出的结果全部正确的概率最大,根据最大似然估计([多元线性回归推理](https://blog.csdn.net/weixin_39445556/article/details/81416133)中有讲过,此处不再赘述),就是所有样本预测正确的概率相乘得到的P(总体正确)最大,此时我们让<img src="https://img-blog.csdnimg.cn/20181110220832633.jpg" alt="img" style="zoom:50%;" /> ,数学表达形式如下:

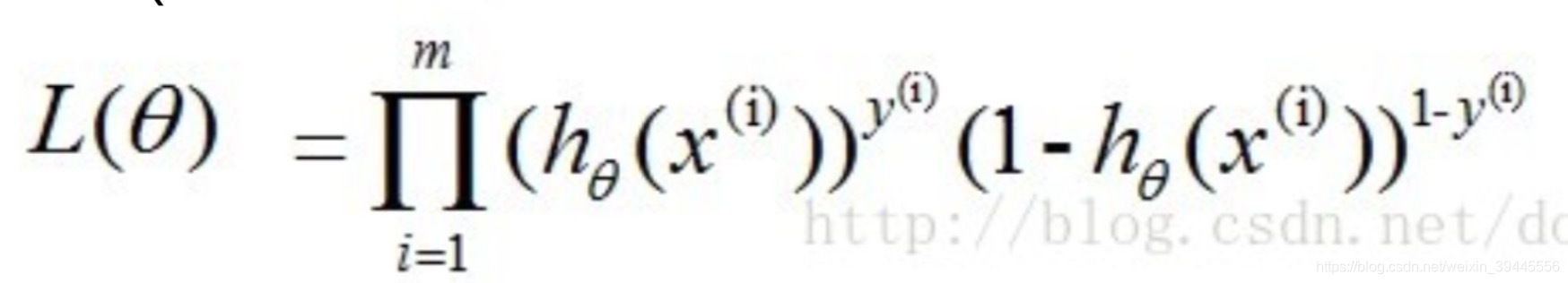
上述公式最大时公式中W的值就是我们要的最好的W.下面对公式进行求解.

我们知道,一个连乘的函数是不好计算的,我们可以通过两边同事取log的形式让其变成连加.

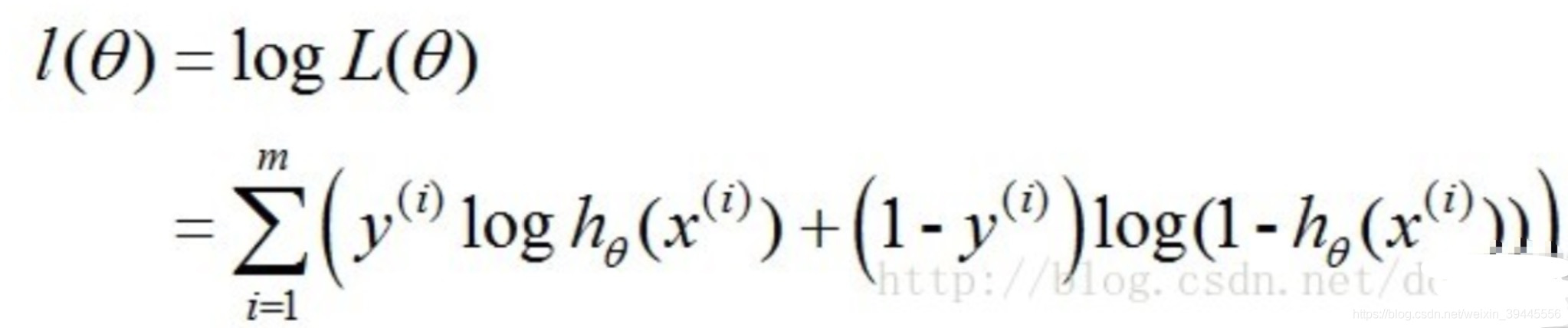
得到的这个函数越大,证明我们得到的W就越好.因为在函数最优化的时候习惯让一个函数越小越好,所以我们在前边加一个负号.得到公式如下:

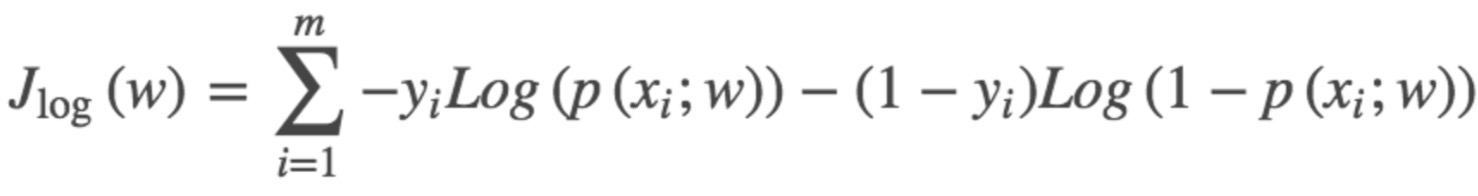
这个函数就是我们逻辑回归(logistics regression)的损失函数,我们叫它交叉熵损失函数.

七.求解交叉熵损失函数

求解损失函数的办法我们还是使用梯度下降,同样在批量梯度下降与随机梯度下降一节有详细写到,此处我们只做简要概括.

求解步骤如下:

1-随机一组W.

2-将W带入交叉熵损失函数,让得到的点沿着负梯度的方向移动.

3-循环第二步.

求解梯度部分同样是对损失函数求偏导,过程如下:

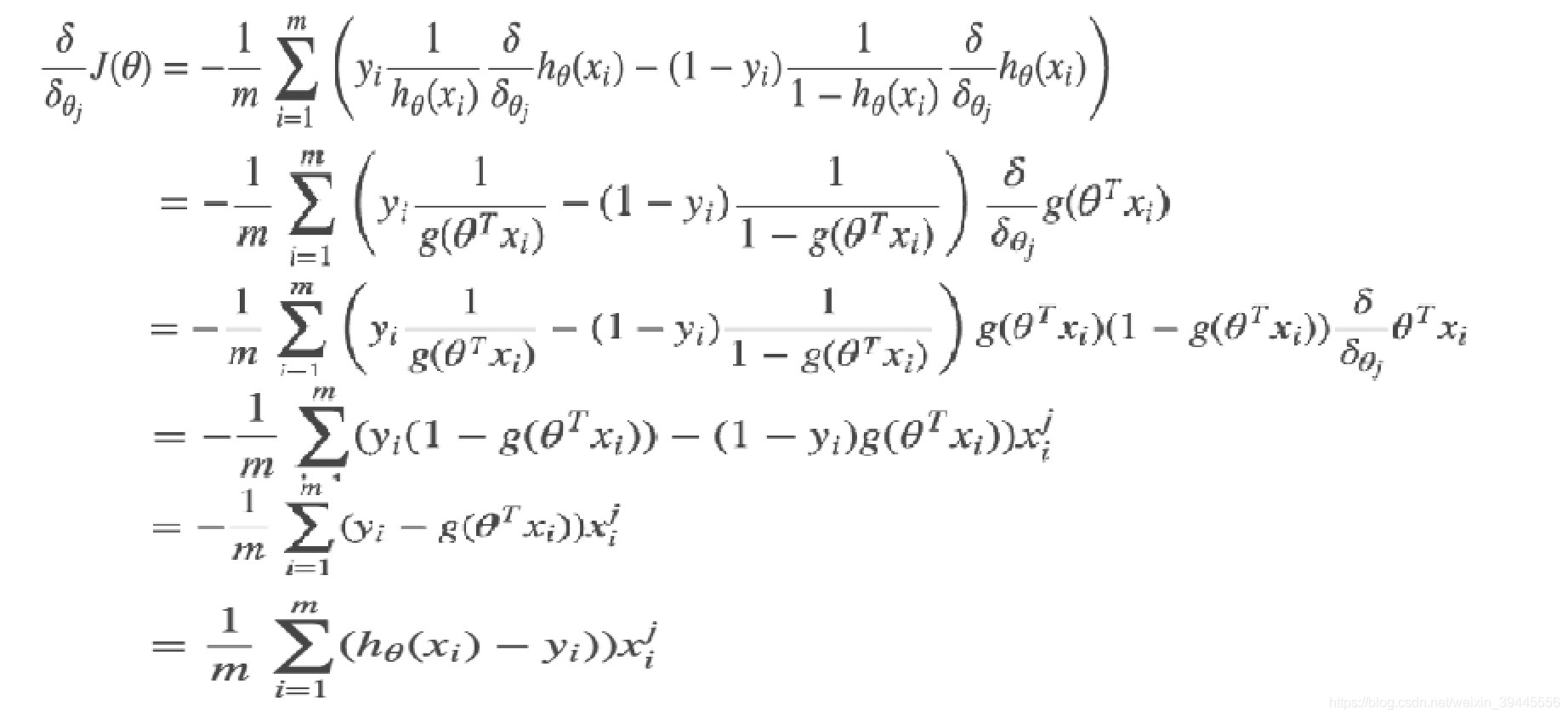
交叉熵损失函数的梯度和最小二乘的梯度形式上完全相同,区别在于,此时的 $h_{\Theta}(x) = g(z)$ 。而最小二乘的 $h_{\Theta} = W^{T}X$

PS:加一个总结:逻辑回归为什么对切斜的数据特别敏感(正负例数据比例相差悬殊时预测效果不好)

首先从文章开头部分举例的两个图可以看到,使用线性模型进行分类第一个要面对的问题就是如何降低离群值的影响,而第二大问题就是,在正负例数据比例相差悬殊时预测效果不好.为什么会出现这种情况呢?原因来自于逻辑回归交叉熵损失函数是通过最大似然估计来推导出的.

使用最大似然估计来推导损失函数,那无疑,我们得到的结果就是所有样本被预测正确的最大概率.注意重点是我们得到的结果是预测正确率最大的结果,100个样本预测正确90个和预测正确91个的两组w,我们会选正确91个的这一组.那么,当我们的业务场景是来预测垃圾邮件,预测黄色图片时,我们数据中99%的都是负例(不是垃圾邮件不是黄色图片),如果有两组w,第一组为所有的负例都预测正确,而正利预测错误,正确率为99%,第二组是正利预测正确了,但是负例只预测出了97个,正确率为98%.此时我们算法会认为第一组w是比较好的.但实际我们业务需要的是第二组,因为正例检测结果才是业务的根本.

此时我们需要对数据进行欠采样/重采样来让正负例保持一个差不多的平衡,或者使用树型算法来做分类.一般树型分类的算法对数据倾斜并不是很敏感,但我们在使用的时候还是要对数据进行欠采样/重采样来观察结果是不是有变好.

————————————————
版权声明：本文为CSDN博主「winrar_setup.rar」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_39445556/article/details/83930186

python代码参考

普通逻辑回归

import numpy
import matplotlib.pyplot as plt

if __name__ == '__main__':
	data = numpy.loadtxt('logicData2.txt', delimiter=',')
    x, y = data[:, :-1], data[:, -1]
    X = (x - numpy.mean(x, axis=0)) / numpy.std(x, axis=0, ddof=1)
    onex, y = numpy.c_[numpy.ones(len(X)), X], numpy.c_[y]
    m, n = onex.shape
    alpha, iter0 = 0.1, 20000
    theta, J = numpy.zeros((n, 1)), numpy.zeros(iter0)
    for i in range(iter0):
        z = numpy.dot(onex, theta)
        h = 1 / (1 + numpy.exp(-z))
        J[i] = (-1 / m) * numpy.sum(y * numpy.log(h) + (1 - y) * numpy.log(1 - h))
        grad = (1 / m) * numpy.dot(onex.T, h - y)	
        theta -= alpha * grad
    print(theta)

多元逻辑回归

import numpy
import matplotlib.pyplot as plt

if __name__ == '__main__':
    data = numpy.loadtxt('logicData2.txt', delimiter=',')
    x, y = data[:, :-1], data[:, -1]
    X = (x - numpy.mean(x, axis=0)) / numpy.std(x, axis=0, ddof=1)
    onex, y = numpy.c_[numpy.ones(len(X)), X], numpy.c_[y]
    m, n = onex.shape
    alpha, iter0 = 0.1, 20000
    theta, J = numpy.zeros((n, 1)), numpy.zeros(iter0)
    for i in range(iter0):
	    z = numpy.dot(onex, theta)
    	h = 1 / (1 + numpy.exp(-z))
		J[i] = (-1 / m) * numpy.sum(y * numpy.log(h) + (1 - y) * numpy.log(1 - h)
 	    grad = (1 / m) * numpy.dot(onex.T, h - y)
        theta -= alpha * grad
	print(theta)
	print(J)

非线性逻辑回归

import numpy
import matplotlib.pyplot as plt

if __name__ == '__main__':
    # 读取数据
	data = numpy.loadtxt('logicData.txt', delimiter=',')
	# 多项式的次数
	d = 3
	# 数据处理
	x, y = data[:, :-1], data[:, -1:]
	# 特征缩放
	X = (x - numpy.mean(x)) / numpy.std(x, axis=0, ddof=1)
	# onex的拼接
	onex = numpy.c_[numpy.ones(len(X))]
	y = numpy.c_[y]
	# onex = numpy.c_[numpy.ones(len(X)), X[:, 0] ** 1, X[:, 0] ** 2, X[:, 0] ** 3]
	# 拼接x1^i
	for i in range(1, d + 1):
    	onex = numpy.c_[onex, X[:, 0] ** i]
	# 拼接x2
	onex = numpy.c_[onex, X[:, 1]]
	m, n = onex.shape
	alpha, iter0 = 0.1, 20000
	theta, J = numpy.zeros((n, 1)), numpy.zeros(iter0)
	# 梯度下降
	for i in range(iter0):
   		z = numpy.dot(onex, theta)  # 公式一
    	h = 1 / (1 + numpy.exp(-z))  # 公式一
    	J[i] = (-1 / m) * numpy.sum(y * numpy.log(h) + (1 - y) * numpy.log(1 - h))  # 公式二
    	grad = (1 / m) * numpy.dot(onex.T, h - y)  # 公式三
    	theta -= alpha * grad  # 公式三
	print(theta)
	print(J)

	count = 0
	for i in range(m):
    	# numpy.where:条件函数，判断h是不是大于0.5.
    	# 如果是，则返回1，如果不是则返回0
    	if (numpy.where(h[i] >= 0.5, 1, 0) == y[i]):
        count += 1
	rate = count / m
	print('分类准确率为{}'.format(rate))

	plt.subplot(121)
	plt.plot(J)
	plt.subplot(122)
	# 利用布尔型索引绘制散点图
	plt.scatter(X[y[:, 0] == 1, 0], X[y[:, 0] == 1, 1], c='r', marker='.')
	plt.scatter(X[y[:, 0] == 0, 0], X[y[:, 0] == 0, 1], c='g', marker='.')
	# 绘制分割线
	x1 = numpy.sort(X[:, 0])
	x2 = numpy.zeros(len(y))
	for i in range(d + 1):
    	x2 += theta[i] * (x1 ** i)
	x2 = -x2 / theta[-1]
	plt.plot(x1, x2, c='r')
	plt.grid(True)
	plt.show()