sigmoid函数与损失函数求导

深度学习：Sigmoid函数与损失函数求导

1、sigmoid函数

sigmoid函数，也就是s型曲线函数，如下：

1.1 从指数函数到sigmoid

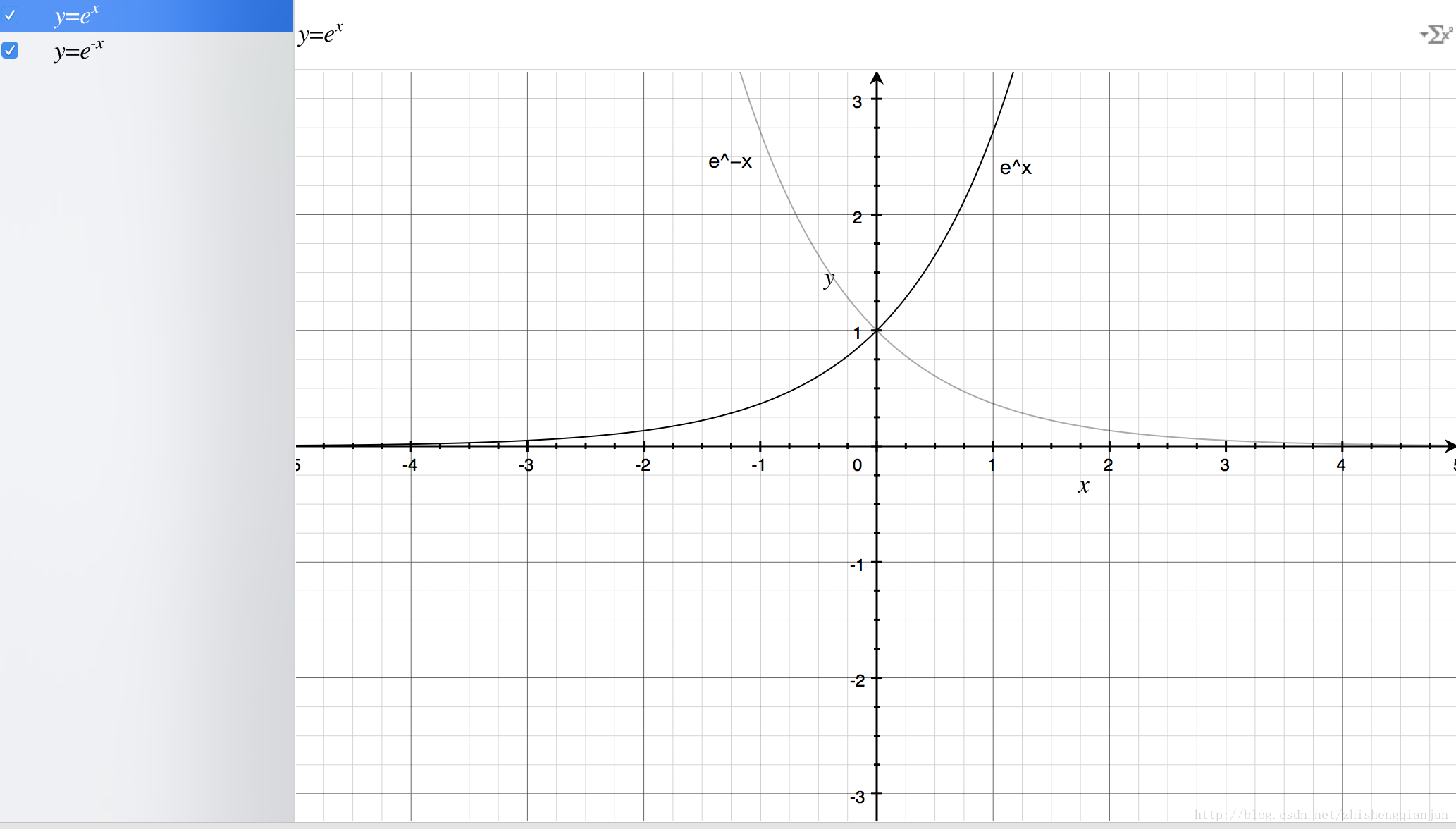
首先我们来画出指数函数的基本图形：

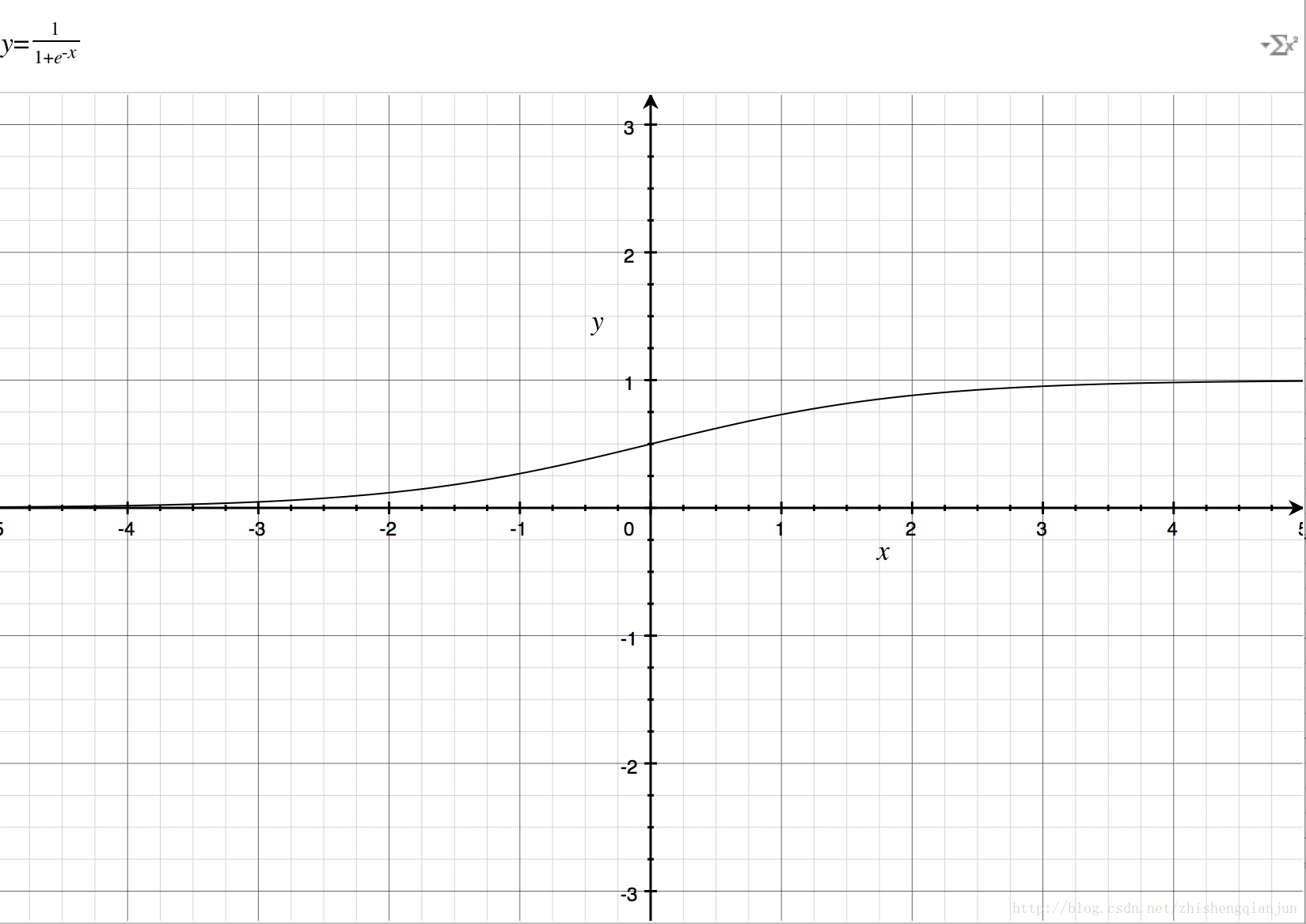
从上图，我们得到了这样的几个信息，指数函数过(0,1)点，单调递增/递减，定义域为(−∞,+∞)，值域为(0,+∞)，再来我们看一下sigmoid函数的图像：

如果直接把e−xe−x放到分母上，就与exex图像一样了，所以分母加上1，就得到了上面的图像，定义域是(−∞,+∞)(−∞,+∞)，值域是(0,1)(0,1)，那么就有一个很好地特性了，就是不管xx是什么，都可以得到(0,1)(0,1)之间的值；

1.2 对数函数与sigmoid

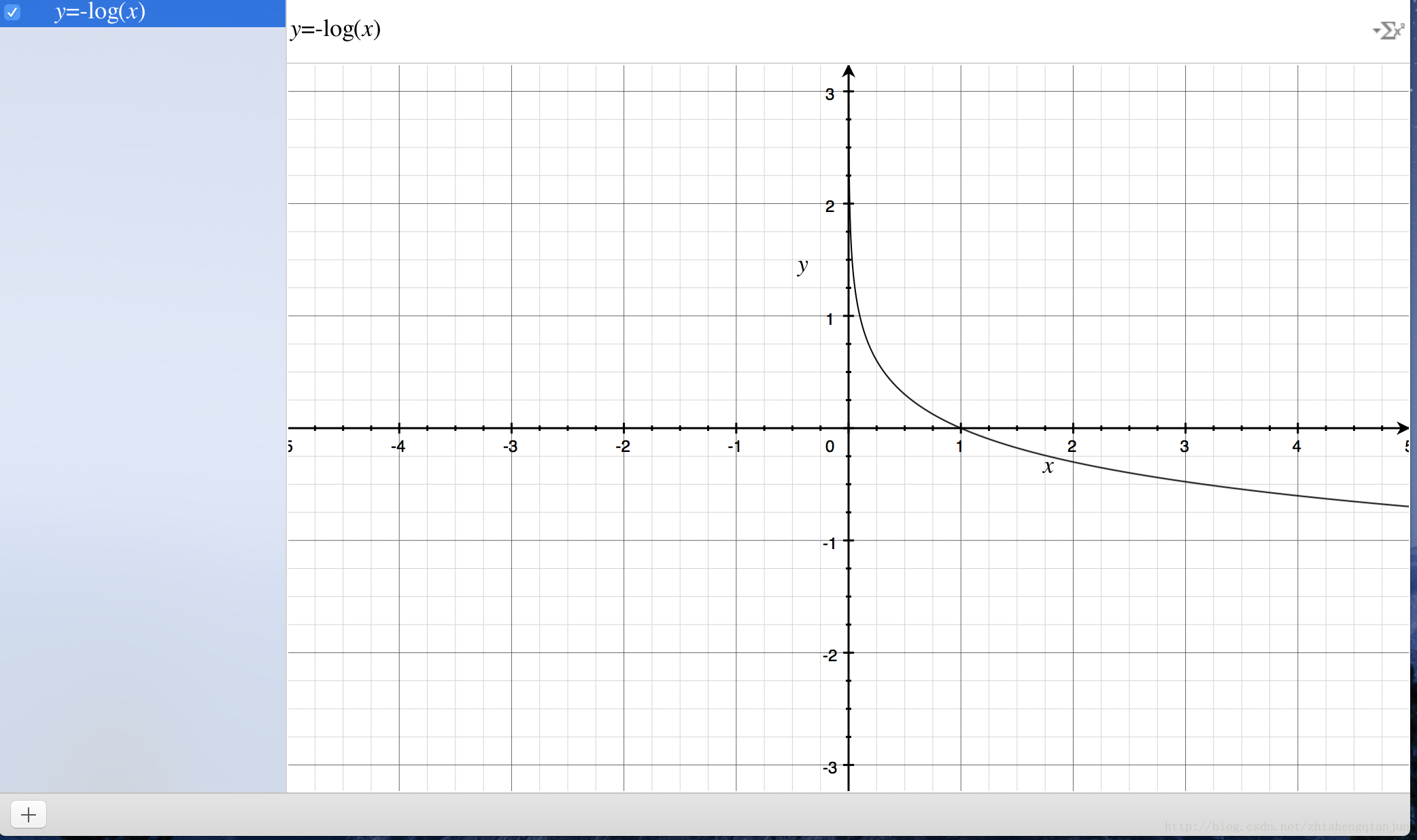
首先来看一下对数函数的图像：

对数函数的图像如上，单调递减，有一个比较好的特性就是在(0,1)(0,1)之间，在接近0的时候，就近无穷大，接近1的时候为0，如果我们把前面的sigmoid函数放到自变量的位置上，就得到了(0,1)(0,1)的图像；

我们如何来衡量一个结果与实际计算值得差距呢？一种思路就是，如果结果越接近，差值就越小，反之越大，这个函数就提供了这样一种思路，如果计算得到的值越接近1，那么那么表示与世界结果越接近，反之越远，所以利用这个函数，可以作为逻辑回归分类器的损失函数，如果所有的结果都能接近结果值，那么就越接近于0，如果所有的样本计算完成以后，结果接近于0，就表示计算结果与实际结果非常相近。

sigmoid函数求导

sigmoid导数具体的推导过程如下：

神经网络损失函数求导

神经网络的损失函数可以理解为是一个多级的复合函数，求导使用链式法则。

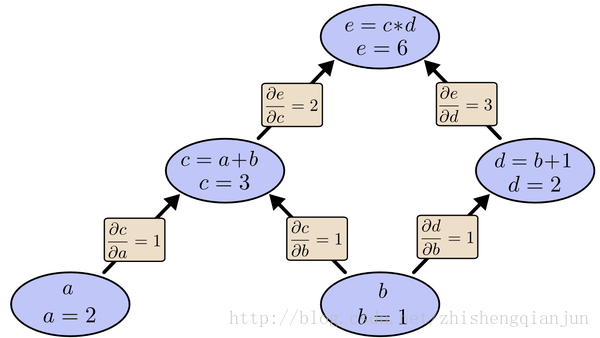
简化复合函数求导：

如上图所示，我们从上往下开始计算，将每个单元的值计算出来，然后计算每个单元的偏导数，保存下来；

接下来继续计算子单元的值，子单元的偏导数，保存下来；将最后的子单元到根节点所在的路径的所有偏导乘起来，就是该函数对这个变量的偏导，计算的本质就是从上往下，计算的时候将值存起来，乘到后面的单元上去，这样每个路径的偏导计算只需要一次，从上到下计算一遍就得到了所有的偏导数。

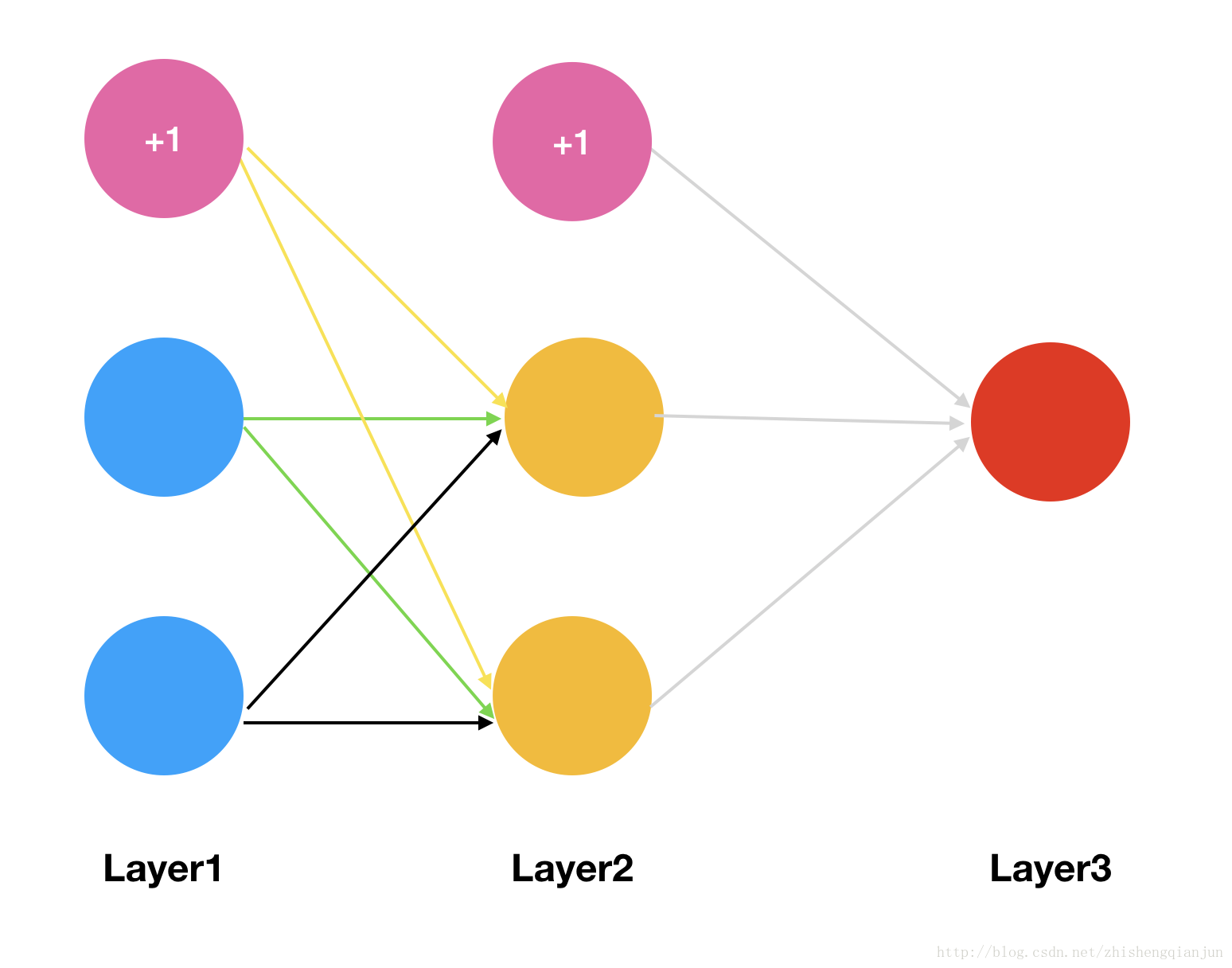
实际上BP(Backpropagation，反向传播算法)，就是如此计算的，如果现在有一个三层的神经网络，有输入、一个隐藏层，输出层，我们对损失函数求权重的偏导数，它是一个复杂的复合函数，如果先对第一层的权重求偏导，然后在对第二层的权重求偏导，会发现，其中有很多重复计算的步骤，就像上面的简单函数的示例，所以，为了避免这种消耗，我们采用的就是从后往前求偏导，求出每个单元的函数值，求出对应单元的偏导数，保存下来，一直乘下去，输入层。

下面用一个简单的示例来演示一下反向传播求偏导的过程：