四类常见的机器学习算法：

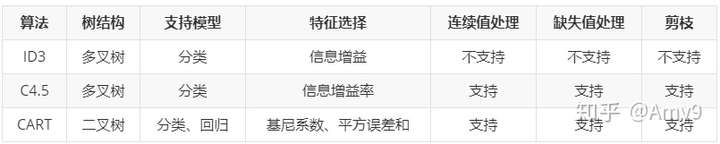
ID3算法：信息增益
C4.5算法：信息增益率
C5.0
CART：基尼系数

首先我们先简单介绍一下决策树，

决策树算法在“决策”领域有着广泛的应用，比如个人决策、公司管理决策等。其实更准确的来讲，决策树算法算是一类算法，这类算法逻辑模型以“树形结构”呈现，因此它比较容易理解，并不是很复杂，我们可以清楚的掌握分类过程中的每一个细节。

if-else原理

想要认识“决策树算法”我们不妨从最简单的“if - else原理”出发来一探究竟。作为程序员，我相信你对 if -else 原理并不感到陌生，它是

条件判断

的常用语句。下面简单描述一下 if -else 的用法：if 后跟判断条件，如果判断为真，也即满足条件，就执行 if 下的代码段，否则执行 else 下的代码段，因此 if-else 可以简单的理解为“如果满足条件就…，否则…”

if-else 有两个特性：一是能够利用 if -else 进行条件判断，但需要首先给出判断条件；二是能无限嵌套，也就是在一个 if-else 的条件执行体中，能够再嵌套另外一个 if-else，从而实现无限循环嵌套。

下面我看一个简单的应用示例，相信你能从中体会到“决策树”的魅力。古人有“伯乐识别千里马”那么“伯乐”是如何“相马”的呢？下表列出了 A、B、C 、D 四匹马，它们具有以下特征：

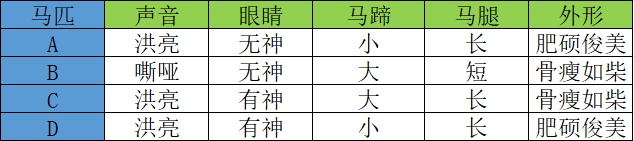
决策树算法

如果你是“伯乐”会如何从中挑选出那匹“千里马”呢？毫无疑问，我们要根据马匹的相应特征去判断，而这些特征对应的值叫做“特征维度值”，下面是一位“伯乐”利用 if -else 原理，最终成功的审识别出“千里马”的全过程，如下所示：

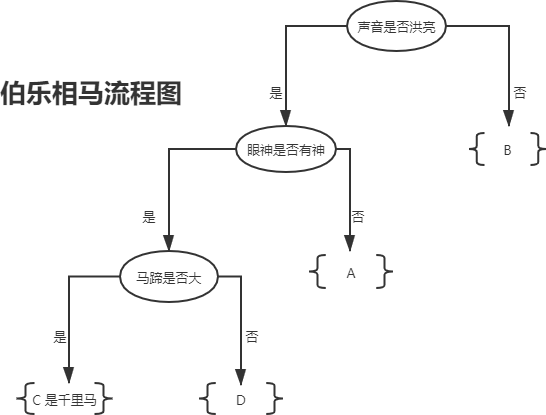
决策树算法
图1：决策树流程图

上图 1 所示是一颗典型的树形结构“二叉树”，而决策树一词中的“树”指的就是这棵树。上图展示了伯乐“识别”千里马的全过程，根据特征值的有无（if-else原理）最终找出“千里马。你可能会问为什么并没囊括所有的特征值？

这是因为某些特征值对于结果的判断而言，并不是最为关键的特征值，比如马的“体型”，“骨瘦如柴”并不能决定某一匹马不是“千里马”。而“马腿”的长短没有作为判断条件，这是因为使用前三个特征值就已经完成了结果的分类，如果此时再使用“马腿”长短作为判断条件，则有点多此一举。

如果将上述判断的流程用 if-else 的伪代码写出来，如下所示：

if (特征值"声音"为"是"):

    if(特征值"眼睛有神"为"是"):

        if (特征值"马蹄大"为"是"):
            类别千里马 C

        else:
            类别普通马匹 D

    else:
        类别普通马匹 A

else:
    类别普通马匹 B

决策树算法关键

了解了“if-else”原理，下面我们进一步认识决策树算法。决策树算法涉及了几个重要的知识点：“决策树的分类方法”，“分支节点划分问题”以及“纯度的概念”。当然在学习过程中还会涉及到“信息熵”、“信息增益”、“基尼指数”的概念，相关知识在后面会逐一介绍。

特征维度&判别条件

我们知道分类问题的数据集由许多样本构成，而每个样本数据又会有多个特征维度，比如前面例子中马的“声音”，“眼睛”都属于特征维度，在决策算法中这些特征维度属于一个集合，称为“特征维度集”。数据样本的特征维度与最终样本的分类都可能存在着某种关联，因此决策树的

判别条件

将从特征维度集中产生。

在机器学习中，决策树算法是一种有监督的分类算法，我们知道机器学习其实主要完成两件事，一个是模型的训练与测试，另外一个是预测数据的（分类问题，预测类别），因此对于决策树算法而言，我们要考虑如何学会自动选择最合适的判别条件，如图 1 所示，只利用前三个特征就完成了分类的预测。这也将是接下来要探讨的重要问题。

纯度的概念

决策树算法引入了“纯度”的概念，“纯”指的是单一，而“度”则指的是“度量”。“纯度”是对单一类样本在子集内所占重的的度量。

在每一次判别结束后，如果集合中归属于同一类别的样本越多，那么就说明这个集合的纯度就越高。比如，二元分类问题的数据集都会被分成两个子集，我们通过自己的纯度就可以判断分类效果的好与坏，子集的纯度越高，就说明分类效果越好。

上一节我们提到过，决策树算法是一类算法，并非某一种算法，其中最著名的决策树算法有三种，分别是 ID3、C4.5 和 CART。虽然他们都属于决策树算法，不过它们之间也存在着一些细微的差别，主要是体现在衡量“纯度”的方法上，它们分别采用了信息增益、增益率和基尼指数，这些算法的相关概念将在后续内容为大家说明。

纯度度量规则

那么我们应该采取什么样的方法去“衡量”某个集合中某一类别样本的纯度呢？当我们学习完机器学习之后，我们总不能还使用人工的方式去验证吧，那可真是徒劳无功了。

要想明确纯度的衡量方法，首先我们要知道一些度量“纯度”的规则。下面我们将类别分为“正类与负类”，如下所示：

某个分支节点下所有样本都属于同一个类别，纯度达到最高值。
某个分支节点下样本所属的类别一半是正类一半是负类，此时，纯度取得最低值。
纯度代表一个类在子集中的占比多少，它并不在乎该类究竟是正类还是负类。比如，某个分支下不管是正类占比 60% 还是负类占比 60%，其纯度的度量值都是一样的。

决策树算法中使用了大量的二叉树进行判别，在一次判别后，最理想的情况是分支节点下包含的类完全相同，也就是说不同的类别完全分开，但有时我们无法只用一个判别条件就让不同的类之间完全分开，因此选择合适判别条件区划分类是我们要重点掌握的。

纯度度量方法

根据之前学习的机器学习算法，如果要求得子集内某一类别所占比最大或者最小，就需要使用求极值的方法。因此，接下来探讨使得纯度能够达到最大值和最小值的“纯度函数”。

1) 纯度函数

现在我们做一个函数图像，横轴表示某个类的占比，纵轴表示纯度值，然后我们根据上面提出的“纯度度量规则”来绘制函数图像：

首先某个类达到最大值，或者最小值时，纯度达到最高值，然后，当某一个类的占比达到 0.5 时，纯度将取得最低值。由这两个条件，我们可以做出 a/b/c 三个点，最后用一条平滑的曲线将这三个点连接起来。如下所示：

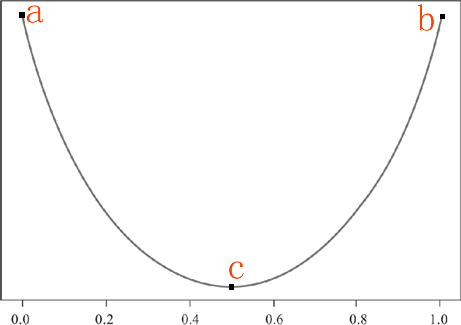
图1：纯度函数图像

如上图，我们做出了一条类似于抛物线的图像，你可以把它看做成“椭圆”的下半部分。当在 a 点时某一类的占比纯度最小，但是对于二元分类来说，一个类小，另一个类就会高，因此 a 点时的纯度也最高（与 b 恰好相反），当某类的纯度占比在 c 点时，对于二元分类来说，两个类占比相同，此时的纯度值最低，此时通过 c 点无法判断一个子集的所属类别。

2) 纯度度量函数

前面在学习线性回归算法时，我们学习了损失函数，它的目的是用来计算损失值，从而调整参数值，使其预测值不断逼近于误差最小，而纯度度量函数的要求正好与纯度函数的要求相反，因为纯度值越低意味着损失值越高，反之则越低。所以纯度度量函数所作出来的图像与纯度函数正好相反。如下图所示：

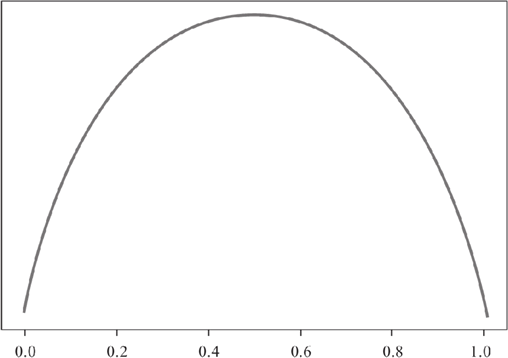
图2：纯度度量函数

上图就是纯度度量函数，它与纯度函数恰好相反。纯度度量函数图像适应于所有决策树算法，比如 ID3、C4.5、CART 等经典算法。

决策树算法原理

决策树特征属性是 if -else 判别条件的关键所在，我们可以把这些特征属性看成一个

集合

，我们要选择的判别条件都来自于这个集合，通过分析与计算选择与待分类样本最合适的“判别条件”。通过前面文章的学习，我们可以知道被选择的“判别条件”使得样本集合的某个子树节点“纯度”最高。

上述过程就好比从众多的样本中提取“类别纯度”最高的样本集合，因此我们可以起一个形象化的名字“提纯”，过程示意图如下所示：

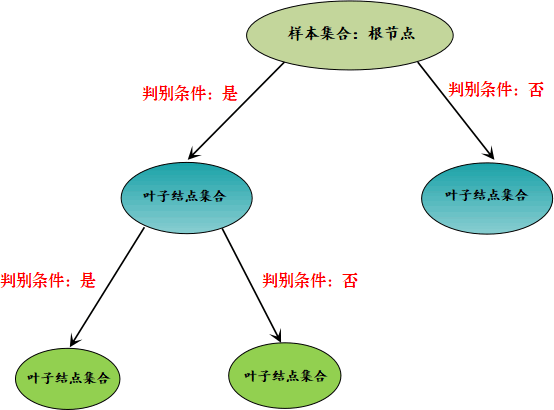
决策树算法流程原理图
图1：决策树流程图

通过上述流程图可以得知，决策树算法通过判别条件从根节点开始分裂为子节点，子节点可以继续分裂，每一次分裂都相当于一次对分类结果的“提纯”，周而复始，从而达到分类的目的，在这个过程中，节点为“否”的不在分裂，判断为“是”的节点则继续分裂。那么你有没有考虑过决策树会在什么情况下“停止”分裂呢？下面列举了两种情况：

1) 子节点属于同一类别

决策树算法的目的是为了完成有效的样本分类。当某个数据集集合分类完成，也就分类后的子节点集合都属于同一个类别，不可再分，此时代表着分类任务完成，分裂也就会终止。

2) 特征属性用完

我们知道，决策树依赖特征属性作为判别条件，如果特征属性已经全部用上，自然也就无法继续进行节点分裂，此处可能就会出现两种情况：一种是分类任务完成，也就是子节点属于同一类别，还有另外一种情况就是分类还没有完成，比如，在判断为“是”的节点集合中，有 8 个正类 3 个负类，此时我们将采用

占比最大的类

作为当前节点的归属类。

3) 设置停止条件

除上述情况外，我们也可以自己决定什么时候停止。比如在实际应用中我们可以在外部设置一些阈值，把决策树的深度，或者叶子节点的个数当做停止条件。

决策树剪枝策略

决策树算法是机器学习中的经典算法。如果要解决分类问题，决策树算法再合适不过了。不过决策树算法并非至善至美，决策树分类算法最容易出现的问题就是“过拟合”。什么是“过拟合”我们在教程的开篇已经提及过，它指的机器学习模型对于训练集数据能够实现较好的预测，而对于测试集性能较差。

“过拟合”使决策树模型学习到了并不具备普遍意义的分类决策条件，从而导致模型的分类效率、泛化能力降低。

决策树出现过拟合的原因其实很简单，因为它注重细节。决策树会根据数据集各个维度的重要性来选择 if -else 分支，如果决策树将所有的特征属性都用完的情况下，那么过拟合现象就很容易出现。

我们知道，每个数据集都会有各种各样的属性维度，总会出现一些属性维度样本分类实际上并不存在关联关系的情况。因此，在理想情况下决策树算法应尽可能少地使用这些不相关属性，但理想终归是理想，在现实情况下很难实现。那么我们要如何解决这种过拟合问题呢？这时就要用到“剪枝策略”。

“剪枝策略”这个名字非常的形象化，它是解决决策树算法过拟合问题的核心方法，也是决策树算法的重要组成部分。剪枝策略有很多种，我们根据剪枝操作触发时间的不同，可以将它们分成两种，一种称为

预剪枝

，另一种称为

后剪枝

。

1) 预剪枝

所谓预剪枝，就是将即将发芽的分支“扼杀在萌芽状态”即在分支划分前就进行剪枝判断，如果判断结果是需要剪枝，则不进行该分支划分。

2) 后剪枝

所谓后剪枝，则是在分支划分之后，通常是决策树的各个判断分支已经形成后，才开始进行剪枝判断。

上述两个剪枝策略，我们重要理解“预”和“后”。“预”就是打算、想要的意思，也就是在分支之前就被剪掉，不让分支生成，而“后”则是以后、后面，也就是分支形成以后进行剪枝操作。那么我要如何判断什么时候需要进行剪枝操作呢？其实很容易理解，如果剪枝后决策树模型在测试集验证上得到有效的提升，就判断其需要剪枝，否则不需要。

剪枝的操作对象是“分支的判别条件”，也就是减少不必要特征属性的介入，从而提高决策树分类效率，和测试集的预测能力。下面通过一个简单的例子进行说明：

某个样本数据集有两个类别（正类与负类），2 个特征属性，现在我们对 20 个样本进行分类。首先，在应用所有“特征属性”的情况下对样本进行分类。如下所示：

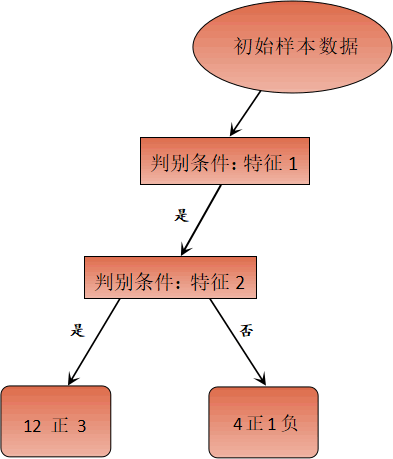
图2：决策树过拟合问题

上图 2 使用了两个特征属性对样本集合进行分类，最后正确分类的概率是 12/20。如果只通过特征 1 进行分类，也就是剪掉冗余特征 2，最后的结果又是怎样呢？如下图所示：

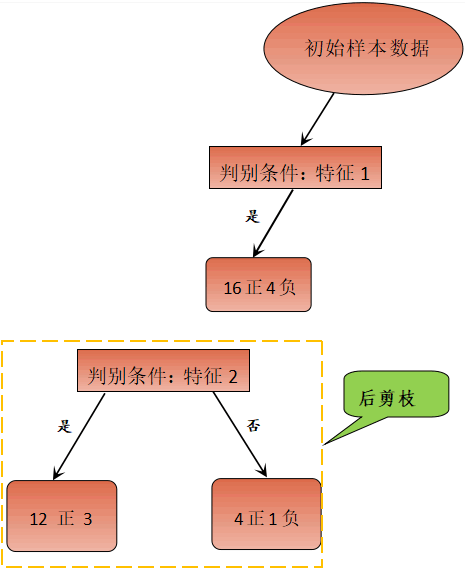
决策树算法后剪枝策略
图3：决策树剪枝策略流程

通过后剪枝策略后，正确分类概率变成了 16/20。显而易见，剪枝策略使得正确分类的概率得到提高。

剪枝策略较容易理解，在实际情况中后剪枝策略使用较多。在分支生成后，使用后剪枝策略将冗余的子树及其判别条件直接剪掉，然后使用上个节点中占比最大的类做为最终的分类结果。

ID3决策树算法

通过前面知识的学习，我们知道决策树算法是以包含所有

类别的集合

为计算对象，并通过条件判别，从中筛选出纯度较高的类别，那么我们如何利用信息熵从特征集合中选择决策条件呢？下面我们以 ID3 算法为例进行说明。

ID3

（Iterative Dichotomiser 3，迭代二叉树3代）算法是决策树算法的其中一种，它是基于

奥卡姆剃刀原理

实现的，这个原理的核心思想就是“大道至简，用尽量少的东西去做更多的事情”。

把上述原理应用到决策树中，就有了 ID3 算法的核心思想：越小型的决策树越优于大的决策树，也就是使用尽可能少的判别条件。ID3 算法使用了信息增益实现判别条件的选择，从香农的“信息论”中可以得知，ID3 算法选择信息增益最大的特征维度进行 if -else 判别。

1) 理解信息增益

那么到底什么是信息增益？我们又如何计算特征维度信息增益值的大小呢？

简单地说，信息增益是针对一个具体的特征而言的，某个特征的有无对于整个系统、集合的影响程度就可以用“信息增益”来描述。我们知道，经过一次 if-else 判别后，原来的类别集合就被被分裂成两个集合，而我们的目的是让其中一个集合的某一类别的“纯度”尽可能高，如果分裂后子集的纯度比原来集合的纯度要高，那就说明这是一次 if-else 划分是有效过的。通过比较使的“纯度”最高的那个划分条件，也就是我们要找的“最合适”的特征维度判别条件。

2) 信息增益公式

那么如何计算信息增益值，这里我们可以采用信息熵来计算。我们通过比较划分前后集合的信息熵来判断，也就是做减法，用划分前集合的信息熵减去按特征维度属性划分后的信息熵，就可能够得到信息增益值。公式如下所示：

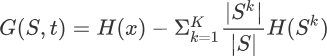
信息增益计算公式

G(S,a) 表示集合 S 选择特征属性 t 来划分子集时的信息增益。H(x) 表示集合的信息熵。上述的“减数”看着有点复杂，下面重点讲解一下减数的含义：

大写字母 K 表示：按特征维度 t 划分后，产生了几个子集的意思，比如划分后产生了 5 个子集吗，那么 K = 5。
小写字母 k 表示：按特征维度 t 划分后，5 个子集中的某一个子集，k = 1 指的是从第一个子集开始求和计算。
|S| 与 |Sk| 表示：集合 S 中元素的个数，这里的||并不是绝对值符号，而 |Sk| 表示划分后，某个集合的元素个数。
|S| /|Sk| 表示：一个子集的元素个数在原集合的总元素个数中的占比，指该子集信息熵所占的权重，占比越大，权重就越高。

最后，比较不同特征属性的信息增益，增益值越大，说明子集的纯度越高，分类的效果就越好，我们把效果最好的特征属性选为 if-else 的最佳判别条件。

ID3 算法是一个相当不错的决策树算法，能够有效解决分类问题，其原理比较容易理解。C4.5 算法是 ID3 算法的增强版，这个算法使用了“信息增益比”来代替“信息增益”，而 CART 算法则采用了“基尼指数”来选择判别条件，“基尼指数”并不同于“信息熵”，但却与信息熵有着异曲同工之妙，这些将作为延伸扩展知识，在后续内容中讲解。

C4.5决策树

C4.5算法是用于生成决策树的一种经典算法，是ID3算法的一种延伸和优化。C4.5算法对ID3算法进行了改进，改进点主要有：

用信息增益率来选择划分特征，克服了用信息增益选择的不足，但信息增益率对可取值数目较少的属性有所偏好；
能够处理离散型和连续型的属性类型，即将连续型的属性进行离散化处理；
能够处理具有缺失属性值的训练数据；
在构造树的过程中进行剪枝；

特征选择

特征选择也即选择最优划分属性，从当前数据的特征中选择一个特征作为当前节点的划分标准。随着划分过程不断进行，希望决策树的分支节点所包含的样本尽可能属于同一类别，即节点的“纯度”越来越高。

具体信息增益相关公式见：ID3算法

信息增益率

信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，C4.5算法采用信息增益率来选择最优划分属性。增益率公式GainRatio(D|A)=infoGain(D|A)IV(A)IV(A)=−∑k=1K|Dk||D|∗log2|Dk||D|

其中 A=[a1,a2,…,ak] ，K个值。若使用A来对样本集D进行划分，则会产生K个分支节点，其中第k个节点包含D中所有属性A上取值为 ak 的样本，记为 Dk 。通常，属性A的可能取值数越多（即K越大），则IV(A)的值通常会越大。

信息增益率准则对可取值数目较少的属性有所偏好。所以，C4.5算法不是直接选择信息增益率最大的候选划分属性，而是先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的。

对连续特征的处理

当属性类型为离散型，无须对数据进行离散化处理；

当属性类型为连续型，则需要对数据进行离散化处理。具体思路如下：

具体思路：

m个样本的连续特征A有m个值，从小到大排列 a1,a2,…,am ，取相邻两样本值的平均数做划分点，一共有m-1个，其中第i个划分点Ti表示为： Ti=(ai+ai+1)/2 。
分别计算以这m-1个点作为二元切分点时的信息增益率。选择信息增益率最大的点为该连续特征的最佳切分点。比如取到的信息增益率最大的点为 at ，则小于 at 的值为类别1，大于 at 的值为类别2，这样就做到了连续特征的离散化。

对缺失值的处理

ID3算法不能处理缺失值，而C4.5算法可以处理缺失值（常用概率权重方法），主要有三种情况，具体如下：

在有缺失值的特征上如何计算信息增益率？

根据缺失比例，折算信息增益（无缺失值样本所占的比例乘以无缺失值样本子集的信息增益）和信息增益率

选定了划分属性，若样本在该属性上的值是缺失的，那么如何对这个样本进行划分？

将样本以不同概率同时划分到不同节点中，概率是根据其他非缺失属性的比例来得到的

对新的样本进行分类时，如果测试样本特性有缺失值如何判断其类别？

走所有分支，计算每个类别的概率，取概率最大的类别赋值给该样本

剪枝

**为什么要剪枝？**因为过拟合的树在泛化能力的表现非常差。

剪枝又分为前剪枝和后剪枝，前剪枝是指在构造树的过程中就知道哪些节点可以剪掉。后剪枝是指构造出完整的决策树之后再来考查哪些子树可以剪掉。

前剪枝

在节点划分前确定是否继续增长，及早停止增长的主要方法有：

节点内数据样本数小于切分最小样本数阈值；
所有节点特征都已分裂；
节点划分前准确率比划分后准确率高。

前剪枝不仅可以降低过拟合的风险而且还可以减少训练时间，但另一方面它是基于“贪心”策略，会带来欠拟合风险。

后剪枝

在已经生成的决策树上进行剪枝，从而得到简化版的剪枝决策树。

C4.5算法采用悲观剪枝方法。根据剪枝前后的误判率来判定是否进行子树的修剪，如果剪枝后与剪枝前相比其误判率是保持或者下降，则这棵子树就可以被替换为一个叶子节点。因此，不需要单独的剪枝数据集。C4.5 通过训练数据集上的错误分类数量来估算未知样本上的错误率。

CART决策树算法

ID3中使用了信息增益选择特征，增益大优先选择。C4.5中，采用信息增益率选择特征，减少因特征值多导致信息增益大的问题。CART分类树算法使用基尼系数选择特征，基尼系数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。这和信息增益（率）相反。

基尼系数

数据集D的纯度可用基尼值来度量

$\begin{aligned} \operatorname{Gini}(D) &=\sum_{i=1}^{n} p\left(x_{i}\right) *\left(1-p\left(x_{i}\right)\right) \\ &=1-\sum_{i=1}^{n} p\left(x_{i}\right)^{2} \end{aligned}$

其中， p(xi) 是分类 xi 出现的概率，n是分类的数目。Gini(D)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。因此，Gini(D)越小，则数据集D的纯度越高。

对于样本D，个数为|D|，根据特征A 是否取某一可能值a，把样本D分成两部分和D1和D2 。所以CART分类树算法建立起来的是二叉树，而不是多叉树。D1=(x,y)∈D|A(x)=a,D2=D−D1

在属性A的条件下，样本D的基尼系数定义为

$\operatorname{GiniIndex}(D \mid A=a)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right)$

对连续特征和离散特征的处理

连续特征

与C4.5思想相同，都是将连续的特征离散化。区别在选择划分点时，C4.5是信息增益率，CART是基尼系数。

具体思路：

m个样本的连续特征A有m个值，从小到大排列 a1,a2,…,am ，则CART取相邻两样本值的平均数做划分点，一共有m-1个，其中第i个划分点Ti表示为： Ti=(ai+ai+1)/2 。
分别计算以这m-1个点作为二元分类点时的基尼系数。选择基尼系数最小的点为该连续特征的二元离散分类点。比如取到的基尼系数最小的点为 at ，则小于 at 的值为类别1，大于 at 的值为类别2，这样就做到了连续特征的离散化。

注意的是，与ID3、C4.5处理离散属性不同的是，如果当前节点为连续属性，则该属性在后面还可以参与子节点的产生选择过程。

离散特征

思路：不停的二分离散特征。

在ID3、C4.5，特征A被选取建立决策树节点，如果它有3个类别A1,A2,A3，我们会在决策树上建立一个三叉点，这样决策树是多叉树，而且离散特征只会参与一次节点的建立。

CART采用的是不停的二分，且一个特征可能会参与多次节点的建立。CART会考虑把特征A分成 A1 和、和、和A2,A3、A2和A1,A3、A3和A1,A2 三种情况，找到基尼系数最小的组合，比如 A2 和 A1,A3 ，然后建立二叉树节点，一个节点是 A2 对应的样本，另一个节点是对 A1,A3 对应的样本。由于这次没有把特征A的取值完全分开，后面还有机会对子节点继续选择特征A划分 A1 和 A3 。

例子

数据集的属性有3个，分别是有房情况，婚姻状况和年收入，其中有房情况和婚姻状况是离散的取值，而年收入是连续的取值。拖欠贷款者属于分类的结果。

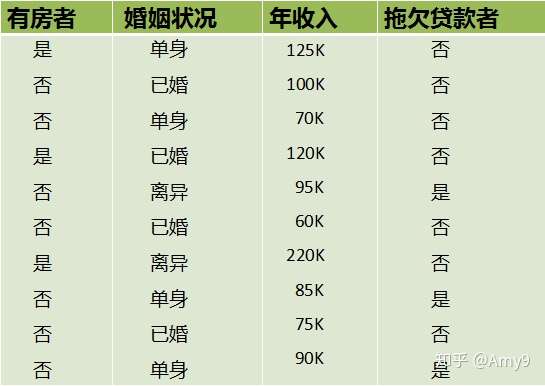
对于有房情况这个属性，它是离散型数据，那么按照它划分后的Gini系数计算如下

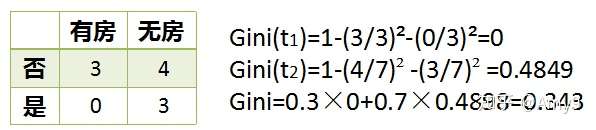
对于婚姻状况属性，它也是离散型数据，它的取值有3种，按照每种属性值分裂后Gini系数计算如下

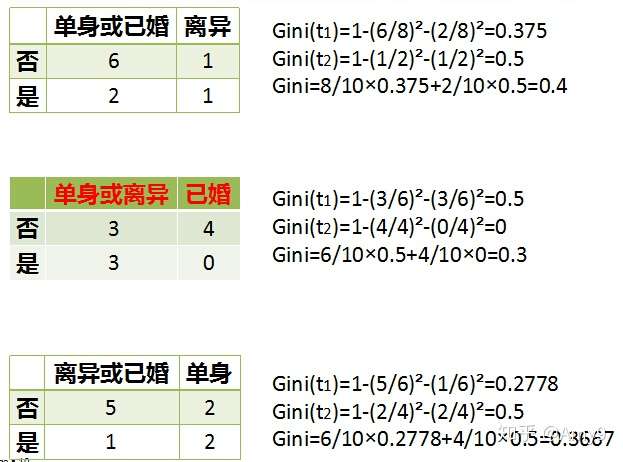
年收入属性，它的取值是连续的，那么连续的取值采用分裂点进行分裂。如下

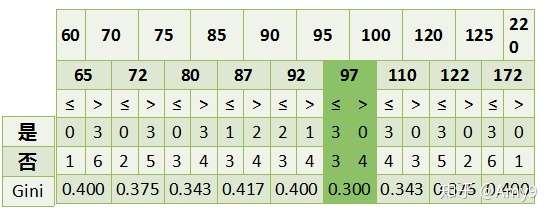
根据这样的分裂规则CART算法就能完成建树过程。

建立CART分类树步骤

输入：训练集D，基尼系数的阈值，切分的最少样本个数阈值

输出：分类树T

算法从根节点开始，用训练集递归建立CART分类树。

对于当前节点的数据集为D，如果样本个数小于阈值或没有特征，则返回决策子树，当前节点停止递归；
计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归；
计算当前节点现有各个特征的各个值的基尼指数，
在计算出来的各个特征的各个值的基尼系数中，选择基尼系数最小的特征A及其对应的取值a作为最优特征和最优切分点。然后根据最优特征和最优切分点，将本节点的数据集划分成两部分 D1 和 D2 ，同时生成当前节点的两个子节点，左节点的数据集为 D1 ，右节点的数据集为 D2 。
对左右的子节点递归调用1-4步，生成CART分类树；

对生成的CART分类树做预测时，假如测试集里的样本落到了某个叶子节点，而该节点里有多个训练样本。则该测试样本的类别为这个叶子节点里概率最大的类别。

剪枝

当分类回归树划分得太细时，会对噪声数据产生过拟合，因此要通过剪枝来解决。剪枝又分为前剪枝和后剪枝，前剪枝是指在构造树的过程中就知道哪些节点可以剪掉。后剪枝是指构造出完整的决策树之后再来考查哪些子树可以剪掉。

在分类回归树中可以使用的后剪枝方法有多种，比如：代价复杂性剪枝、最小误差剪枝、悲观误差剪枝等等。这里只介绍代价复杂性剪枝法。

对于分类回归树中的每一个非叶子节点计算它的表面误差率增益值α

α=C(t)−C(Tt)|Tt|−1

|Tt| :子树中包含的叶子节点个数

C(t)：以t为单节点树的误差代价，该节点被剪枝

C(t)=r(t)∗p(t)

r(t)：节点t的误差率

p(t)：节点t上的数据占所有户数的比例

C(Tt) 是以t为根节点的子树 Tt 的误差代价，如果该节点不被剪枝，它等于子树 Tt 上所有叶子节点的误差代价之和。

比如有个非叶子节点T4如图所示：

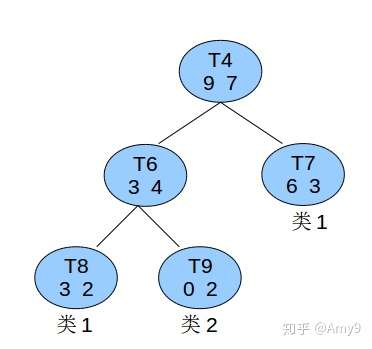
已知所有的数据总共有60条，则节点T4的节点误差代价为：C(t)=r(t)p(t)=7161660=760

子树误差代价为：C(Tt)=∑C(i)=25560+02260+39∗960=560

以T4为根节点的子树上叶子节点有3个，则α=7/60−5/603−1=160

找到 α 值最小的非叶子节点，令其左、右子节点为NULL。当多个非叶子节点的α值同时达到最小时，取 |Tt| 最大的进行剪枝。

决策树算法补充