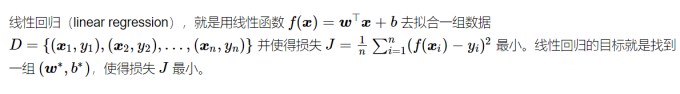岭回归和LASSO回归，线性回归

线性回归很简单，用线性函数拟合数据，用 mean square error (mse) 计算损失（cost），然后用梯度下降法找到一组使 mse 最小的权重。

lasso 回归和岭回归（ridge regression）其实就是在标准线性回归的基础上分别加入 L1 和 L2 正则化（regularization）。

本文的重点是解释为什么 L1 正则化会比 L2 正则化让线性回归的权重更加稀疏，即使得线性回归中很多权重为 0，而不是接近 0。或者说，为什么 L1 正则化（lasso）可以进行 feature selection，而 L2 正则化（ridge）不行。

线性回归——最小二乘

线性回归的拟合函数（或 hypothesis）为：

$$f(x) = w^Tx+b$$

cost function (mse) 为：

$$\begin{aligned} J &=\frac{1}{n} \sum_{i=1}^{n}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2} \\ &=\frac{1}{n} \sum_{i=1}^{n}\left(\boldsymbol{w}^{\top} \boldsymbol{x}_{i}+b-y_{i}\right)^{2} \end{aligned}$$

Lasso回归和岭回归

Lasso 回归和岭回归（ridge regression）都是在标准线性回归的基础上修改 cost function，即修改式（2），其它地方不变。

Lasso 的全称为 least absolute shrinkage and selection operator，又译最小绝对值收敛和选择算子、套索算法。

Lasso 回归对式（2）加入 L1 正则化，其 cost function 如下：

$$J=\frac{1}{n} \sum_{i=1}^{n}\left(f\left(x_{i}\right)-y_{i}\right)^{2}+\lambda\|w\|_{1}$$

岭回归对式（2）加入 L2 正则化，其 cost function 如下：

$$J=\frac{1}{n} \sum_{i=1}^{n}\left(f\left(x_{i}\right)-y_{i}\right)^{2}+\lambda\|w\|_{2}^2$$

Lasso回归和岭回归的同和异：

• 相同：
  • 都可以用来解决标准线性回归的过拟合问题。
• 不同：
  • lasso 可以用来做 feature selection，而 ridge 不行。或者说，lasso 更容易使得权重变为 0，而 ridge 更容易使得权重接近 0。
  • 从贝叶斯角度看，lasso（L1 正则）等价于参数 ww 的先验概率分布满足拉普拉斯分布，而 ridge（L2 正则）等价于参数 ww 的先验概率分布满足高斯分布。具体参考博客 从贝叶斯角度深入理解正则化 – Zxdon 。

也许会有个疑问，线性回归还会有过拟合问题？

加入 L1 或 L2 正则化，让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。

可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什幺影响，一种流行的说法是『抗扰动能力强』。具体参见博客 浅议过拟合现象(overfitting)以及正则化技术原理。

References

[1] Tibshirani, R. (1996). Regression Shrinkage and Selection Via the Lasso. Journal Of The Royal Statistical Society: Series B (Methodological), 58(1), 267-288. doi: 10.1111/j.2517-6161.1996.tb02080.x
[2] Lasso算法 – 维基百科
[3] 机器学习总结(一)：线性回归、岭回归、Lasso回归 – 她说巷尾的樱花开了
[4] 从贝叶斯角度深入理解正则化 – Zxdon
[5] 浅议过拟合现象(overfitting)以及正则化技术原理 – 闪念基因

线性回归——lasso回归和岭回归（ridge regression） - wuliytTaotao - 博客园 (cnblogs.com)