K折交叉验证

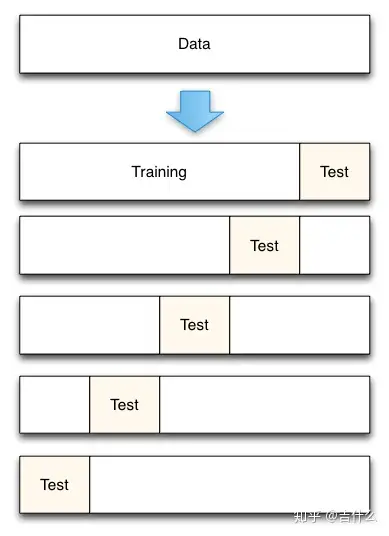
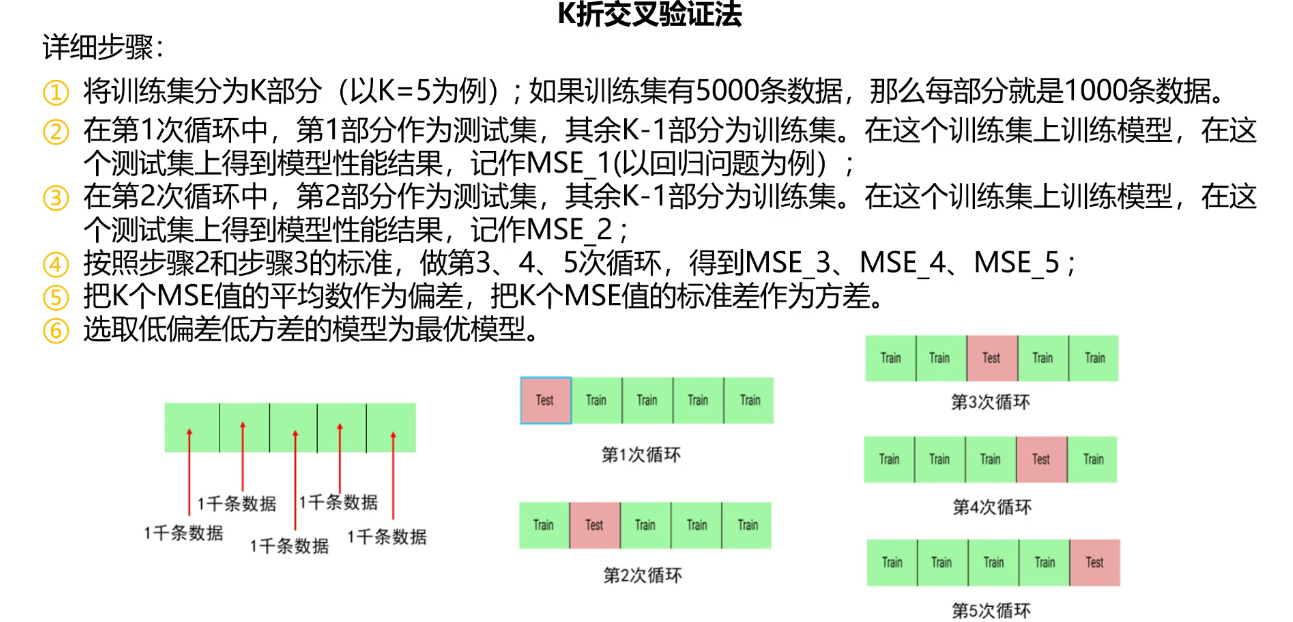
K-Fold Cross Validation K折交叉验证，将原始数据分成K组（一般是均分），将每个子集数据分别做一次测试集，其余K-1组子集数据作为训练集。这样可得到K个模型/

用这K个模型最终在验证集的评估指标分数（如准确率、R2）平均数作为偏差，评估指标分数的标准差作为方差。

静态的「留出法」对数据的划分方式比较敏感，有可能不同的划分方式得到了不同的模型。「k 折交叉验证」是一种动态验证的方式，这种方式可以降低数据划分带来的影响。具体步骤如下：

将数据集分为训练集和测试集，将测试集放在一边
将训练集分为 k 份
每次使用 k 份中的 1 份作为验证集，其他全部作为训练集。
通过 k 次训练后，我们得到了 k 个不同的模型。
评估 k 个模型的效果，从中挑选效果最好的超参数
使用最优的超参数，然后将 k 份数据全部作为训练集重新训练模型，得到最终模型。

1.使用 train/test split 进行模型评估的缺点

Train/test split 是将原始数据集划分为训练集/测试集，避免了为了追求高准确率而在训练集上产生过拟合，从而使得模型在样本外的数据上预测准确率高。

但是，划分出训练集/测试集的不同会使得模型的准确率产生明显的变化。以上一篇 iris 为例：

# 使用 train/test split, random_state=4
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=4)

# 评估模型的分类准确率
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
print(knn.score(X_test, y_test))
```
0.973684210526
```

# 改变 random_state=3
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=3)

# 评估模型的分类准确率
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X_train, y_train)
print(knn.score(X_test, y_test))
```
0.947368421053
```

为了消除这一变化因素，我们可以创建一系列训练集/测试集，计算模型在每个测试集上的准确率，然后计算平均值。

这就是 K-fold cross-validation 的本质**。**

2. K-fold cross-validation 如何克服这些缺点

K-fold cross-validation的步骤：

将原始数据集划分为相等的K部分（“折”）
将第1部分作为测试集，其余作为训练集
训练模型，计算模型在测试集上的准确率
每次用不同的部分作为测试集，重复步骤2和3 K次
将平均准确率作为最终的模型准确率

5-fold cross-validation

模拟5-fold cross-validation：

from sklearn.cross_validation import KFold
kf = KFold(25, n_folds=5, shuffle=False)

# 打印每个训练集和测试集
print('{} {:^61} {}'.format('Iteration', 'Training set observations', 'Testing set observations'))
for iteration, data in enumerate(kf, start=1):
    print('{:^9} {} {:^25}'.format(iteration, str(data[0]), str(data[1])))

the contents of each training and testing set

原始数据包含25个样本
5折交叉验证运行了5次迭代
每次迭代，每个样本只在训练集中或者测试集中
每个样本只在测试集中出现一次

对比 cross-validation 和 train/test split 可以发现：

cross-validation 对于样本外数据有更高的准确率
cross-validation 更有效的发挥样本的作用

3. K-fold cross-validation 如何用于参数调优以及选择模型和特征

以 KNN 模型为例，当 KNN 的 K=5 时， 10-fold cross-validation （K-fold cross-validation 的 K 可以选择任意整数，但通常选择10，这是实践中效果最好的值）过程如下：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.cross_validation import cross_val_score

# 实例化KNN模型,KNN的K=5
knn = KNeighborsClassifier(n_neighbors=5)
# 10-fold cross-validation,cv=10
scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
print(scores)
```
[ 1.          0.93333333  1.          1.          0.86666667  0.93333333
  0.93333333  1.          1.          1.        ]
```

# 计算平均值
print(scores.mean())
```
0.966666666667
```

注意：cross_val_score() 传入的 X 和 y 是原始特征和标签，而非经过 train/test split 的训练集。划分过程由 cross_val_score() 函数内完成。

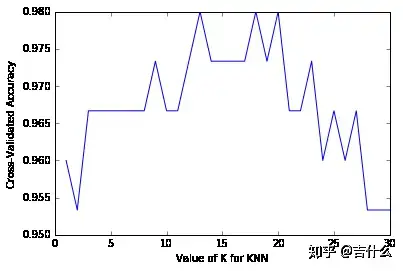
利用 10-fold cross-validation 寻找 KNN 模型中效果最好的 K：

k_range = list(range(1, 31))  # K的范围[1, 30]
k_scores = []  # 存放每个K的评价结果
for k in k_range:
    knn = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn, X, y, cv=10, scoring='accuracy')
    k_scores.append(scores.mean())
print(k_scores)
```
[0.95999999999999996, 0.95333333333333337, 0.96666666666666656, 
0.96666666666666656, 0.96666666666666679, 0.96666666666666679, 
0.96666666666666679, 0.96666666666666679, 0.97333333333333338, 
0.96666666666666679, 0.96666666666666679, 0.97333333333333338, 
0.98000000000000009, 0.97333333333333338, 0.97333333333333338, 
0.97333333333333338, 0.97333333333333338, 0.98000000000000009, 
0.97333333333333338, 0.98000000000000009, 0.96666666666666656, 
0.96666666666666656, 0.97333333333333338, 0.95999999999999996, 
0.96666666666666656, 0.95999999999999996, 0.96666666666666656, 
0.95333333333333337, 0.95333333333333337, 0.95333333333333337]
```

# 将结果可视化
import matplotlib.pyplot as plt
%matplotlib inline

# plot the value of K for KNN (x-axis) versus the cross-validated accuracy (y-axis)
plt.plot(k_range, k_scores)
plt.xlabel('Value of K for KNN')
plt.ylabel('Cross-Validated Accuracy')

准确率最高的 KNN 的 K的范围是[13, 20]，整个曲线的形状是倒U形。考虑偏差方差平衡，偏低的K值产生低偏差和高方差，较高的K值产生高偏差和低方差，最好的模型K值应折中，以平衡偏差和方差。

在 KNN 模型中，通常建议选择使得模型最简单的K值，越高的K会使模型复杂性越低，因此此例中选择 K=20 作为最好的 KNN 模型。

4. K-fold cross-validation 可能的改进措施

重复利用不同的随机分组数据进行交叉验证
降低交叉验证单一方案的方差来提高样本外的预测准确率
将原始数据中的一部分数据设置为 “hold-out set”，在其余部分进行 CV 的整个过程，但模型最终准确率为模型在 hold-out set 上的准确率，因为 hold-out set 相当于样本外的数据