数据预处理概念

数据预处理概念篇

数据预处理的目的是，对原始数据进行预处理，以提高数据质量，提高学习算法的准确性、有效性和可伸缩性，达到简化学习模型和提高算法的泛化能力。

常用的数据预处理技术包括：

• 数据清理
• 数据变换
• 数据归约
• 数据离散化
• 特征选择

1、数据集类型

三个重要特征

• 维度：数据集中的对象具有的属性个数总合
• 稀疏性：有意义数据的占比。
• 分辨率：观察深度。

三类数据集：

• 记录数据：
  • 事物数据/购物篮数据
  • 数据矩阵
• 基于图形的数据
• 有序数据：
  • 时序数据：
  • 序列数据：生物学序列，购物单
  • 时间序列数据：股票，库存控制
  • 空间数据：空间自相关，地理系统，医学图像
  • 流数据：电力供应，银行

2、数据统计特性

数据统计又称为汇总统计

中心趋势度量：

均值（mean）

算术均值：

$$\overline{x} = \frac{\sum_{i=1}^{N}{x_i}}{N} = \frac{x_1 + x_2 + \ldots + x_N}{N}$$

加权算数均值（带权重）：

$$\overline{x} = \frac{\sum_{i=1}^{N}{w_ix_i}}{\sum_{i=1}^{N}{w_i}} = \frac{w_1x_1 + w_2x_2 + \ldots + w_Nx_N}{w_1+w_2 + \ldots + w_N}$$

截断均值：

指定0~100内的百分位数p，丢弃高端低端的2%的数据再计算均值。

中位数（median）

有序集的中间值，偶数集中是中间两个值的平均值。

众数（mode）

集合中出现频率最高的值。

中列数（midrange）

中列数可用来评估数据集的中心趋势，是数据集的最大最小值的平均值。

极差：

max - min

方差：

$$S_x^2 = \frac{1}{m-1} \sum_{i=1}^{m}{(x - \overline{x})^{2}}$$

3、数据清理

（1）缺失值处理

• 忽略元组，即放弃该单位
• 忽略属性列：放弃该属性
• 人工填写缺失值：
• 自动填充缺失值：
  • 0填充：全部补0。
  • 众数/中位数/均值：根据数据情况大致填充。
  • 常数填充：自己设定一个常数填充。
  • 基于回归/推理/决策树：更高级的做法，代价大

（2）噪声数据平滑方法

建议先绘制箱型图，检验正态分布。

• 3sigma原则：若数据集满足正态分布，则可根据3sigma原则淘汰离群点。

如果数据服从正态分布，在3σ原则下，异常值被定义为一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布下，距离平均值3σ之外的值出现的概率为 P(|x-μ|>3σ)<=0.003，属于极个别的小概率事件。如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。

​ 如果数据不服从正态分布，那么可以用远离平均值的多少倍标准差来描述，倍数就是Z-score。Z-score以标准差为单位去度量某一原始分数偏离平均数的距离，它回答了一个问题：“一个给定分数距离平均数多少个标准差?”，Z-score的公式是：

$$Z = \frac{X -\mu }{\sigma}$$

• IQR方法：四分位点内距是指在第75个百分点与第25个百分点的差值，或者说，上、下四分位数之间的差，计算IQR的公式是：

$$IQR = Q3 − Q1$$

IQR是统计分散程度的一个度量，分散程度通过需要借助箱线图来观察，通常把小于 Q1 - 1.5 * IQR 或者大于 Q3 + 1.5 * IQR的数据点视作离群点，探测离群点的公式是：

$$outliers = value < ( Q1 - 1.5 * IQR ) or value > ( Q3 + 1.5 * IQR )$$

• 箱型图分析法：一般采用此方法分析异常值

箱线图可以直观地看出数据集的以下重要特性：

中心位置：中位数所在的位置就是数据集的中心，从中心位置向上或向下看，可以看出数据的倾斜程度。
散布程度：箱线图分为多个区间，区间较短时，表示落在该区间的点较集中；
对称性：如果中位数位于箱子的中间位置，那么数据分布较为对称；如果极值离中位数的距离较大，那么表示数据分布倾斜。
离群点：离群点分布在箱线图的上下边缘之外。

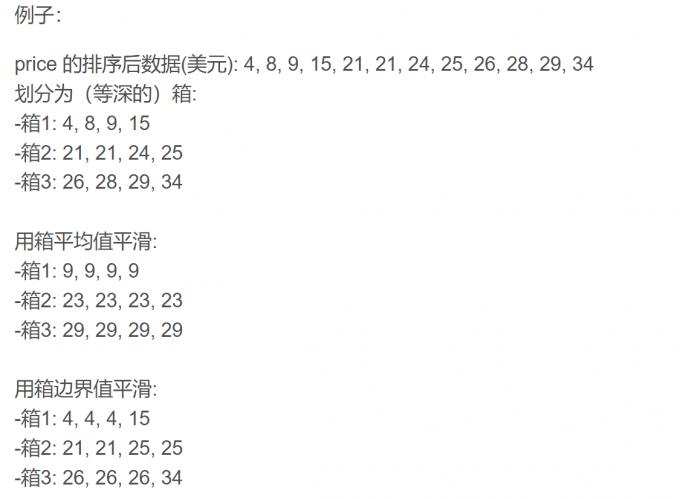
• 分箱：等深分箱法、等宽分箱法、最小熵法和用户自定义区间法。
• 数据平滑方法：有3种
  • 按平均值平滑：对同一箱值中的数据求平均值，用平均值替代该箱子中的所有数据
  • 按边界值平滑：用距离较小的边界值替代箱中每一数据
  • 按中值平滑：取箱子的中值，用来替代箱子中的所有数据。

数据挖掘如何分箱以及如何对每个箱子中的数据进行平滑处理

python分箱法

• **聚类：**聚类将类似的值组织成群或”簇“。离群点可以被聚类检测，直观地，落在簇集合之外的值被视为异常值。通过删除离群点来平滑数据。
• **回归：**线性非线性回归来拟合函数平滑数据。

4、数据聚合

将冗余数据删除，如一个人的出生年龄和出生日期。

一般根据具体特征意义来进行聚合。

5、数据变换

数据转换的方法有下面三种：

• 数据泛化（Data Generalization）：将底层数据抽象到更高的概念层。
• 数据标准化（Data Standardization）：将数据按比例缩放，使数据都落在一个特定的区间
• 数据离散化（Data Discretization）：将数据用区间或者类别的概念替换。

数据泛化

从概念上讲，数据立方体可以看做一种多维数据泛化。数据泛化通过把相对低层的值（例如，属性年龄的数值）用较高层概念（例如，青年、中年和老年）替换来汇总数据。

• 数据特征化的面向属性的归纳
• 面向属性归纳的有效实现
• 类比较的面向属性归纳

数据规范化

是原来的度量值转换为无量纲的值。对于使用距离度量的分类方法，如神经网络，KNN分类和聚类算法，规范化起到很好的效果。

对于基于距离的方法，规范化可以帮助平衡具有较大初始值域的属性与具有较小初始值域的属性可比性。

常见方法：

（1）最小-最大规范化

$$Z_{ij} = \frac{x_{ij}- min_{f}}{max_{f}-min{f}}(b-a) + a$$

做了线性变换，将值转换至[a,b]中

最小-最大规范化保持原有数据，若产生新的数据，会发生“越界错误”。

（2）z-score规范化

其中EX为评价值，sigma为标准差。

$$Z_{if} = \frac{x_{if} - EX_f}{\sigma_f}$$

（3）小数点定标规范化

特征构造

特征提取，指标建立

数据离散化

等宽等频离散化。

比如：5，10，15，19，24

变化为：1，2，3，4，5。以5为宽

基于聚类分析的离散化。

基于熵的离散化。

数据归约

维度规约 是指通过使用数据编码或变换，得到原始数据的归约或“压缩”表示。

维归约的好处：

• 降低时间空间复杂度
• 模型更容易理解

离散小波变换（DWT )

离散傅里叶变换

主成分分析（PCA)

抽样

特征选择

​ 特征选择是指从一组已知特征集合中选择最具有代表性的特征子集，使其保留原有数据的大部分信息，即选择的特征子集可以像原来的全部特征一样用来正确区分数据集中的每个数据对象。

分为三种方法：过滤，，封装，嵌入