论文跟读(一)反向传播
论文跟读系列(一):反向传播
资源
https://www.iro.umontreal.ca/~vincentp/ift3395/lectures/backprop_old.pdf
【【论文必读#1:反向传播】在错误中学习,在传递中演进】 https://www.bilibili.com/video/BV1954y1o7bh/?share_source=copy_web&vd_source=bd967f0d540a64617b8b612bc0f0f9a3
作者介绍
这篇论文是三位大牛的合作,其中有我们比较了解的Hinton大牛。
知识点
反向传播入门
- 神经网络15分钟入门!——反向传播到底是怎么传播的? - Mr.看海的文章 - 知乎
https://zhuanlan.zhihu.com/p/66534632 - 反向传播最佳总结——一篇文章读懂神经网络反向传播 - 干好每一天的文章 - 知乎
https://zhuanlan.zhihu.com/p/662487898 - 温故知新——前向传播算法和反向传播算法(BP算法)及其推导 - G-kdom的文章 - 知乎
https://zhuanlan.zhihu.com/p/71892752 - 【[5分钟深度学习] #02 反向传播算法】https://www.bilibili.com/video/BV1yG411x7Cc?vd_source=bd967f0d540a64617b8b612bc0f0f9a3
其实大部分内容,知乎或者CSDN的内容会很详细,而且是中文的带图片。在我之前的博客也有记载。这里不多介绍。这篇文章是深度学习基础中的基础,看视频也好,读原文也好,要读懂反向传播的全流程,对神经网络的学习大有收益。
专业英语
- Learning representations by back-propagating errors:在反向传播的误差中进行学习。
- BP:back-propagating 反向传播
- learning procedure:学习方法
- self-organizing neural networks:自训练神经网络
- symmetrical pattern:对称图案
- perceptron:感知机
出发点,目的
反向传播与感知机来说,他能够发现新的特征(features),来自代价函数的信息通过网络向后流动,以便计算梯度。本质上,他只是用来计算梯度的。
方法,创新
链式法则是反向传播的基本传递方式,它大大简化了反向传播计算的复杂程度。对反向传播算法的过程进行一下总结:
**输入:**总层数L,以及各隐藏层与输出层的神经元个数,激活函数,损失函数,迭代步长 α\alpha ,最大迭代次数MAX与停止迭代阈值 ϵ\epsilon ,输入的m个训练样本 ((x1,y1),(x2,y2),…(xm,ym))((x_{1},y_{1}),(x_{2},y_{2}),…(x_{m},y_{m}))
1. 初始化参数W,b
2. 进行前向传播算法计算,for l=2l=2 to L
z(l)=W(l)a(l−1)+b(l)z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)}
a(l)=σ(z(l))a^{(l)}=\sigma(z^{(l)})
3. 通过损失函数计算输出层的梯度
4. 进行反向传播算法计算,for l=L−1l=L-1 to 2
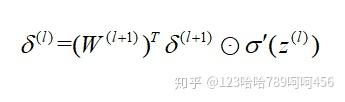
5. 更新W,b
通过梯度下降算法更新权重ww和偏置bb的值,α\alpha为学习率其中α∈(0,1]\alpha\in(0,1]。

6. 如果所有W,b的变化值都小于停止迭代阈值ϵ,则跳出迭代循环
7. 输出各隐藏层与输出层的线性关系系数矩阵W和偏置b。
结果,贡献
从另一个角度理解深度学习:通过多层处理,逐渐将初始的”低层”特征表示转化为“高层”特征表示后,用“简单模型”即可完成复杂的分类等学习任务,由此可将深度学习理解为进行特征学习或表示学习。





