排队论
排队论
零.排队论简述
什么是排队论:
排队论(queueing theory)是专门研究带有随机因素产生拥挤现象的优化理论,是有关于服务设施与被服务者构成的排队服务系统的理论。
亦称随机服务系统理论。因为被服务者到达系统的时间是不确定的。
排队论是计算机通信网络和计算机系统中通信信息量研究的基础理论,信息系统通信问题的定量研究往往要求借助于排队论才能得到解决。
经典模型:
一.基本组成
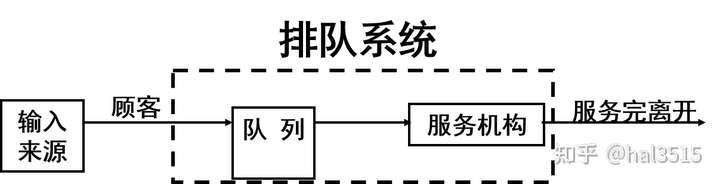
1.输入过程
顾客到达的方式通常是一个给一个到达的,也可能是成批的。顾客到达总是有一定规律,即到达的过程或到达时间间隔符合一定的分布,称到达分布。
顾客到达或到达时间通常假定为相互独立的且遵从同一分布的随机变
- 顾客来源:有限/无限
- 顾客数量:有限/无限
- 经常性的顾客来源:顾客到达间隔时间服从某一概率分布
- 顾客的行为假定:在未服务之前不会离开、当看到队列很长的时候离开、从一个队列移到另一个队列
2.服务规则
- 服务规则
- 服务台数量:单服务台、多服务台、无限服务台
- 服务协议:FCFS、LCFS、RSS、PR、PS、IS
- 先来先服务:FCFS(First-Come-First-Served)
- 后来后服务:LCFS(Last-Come-First-Served)队列是一种堆栈形式,如果队列中有两个以上等待的顾客,则把最后到达的顾客作为下一个服务对象。
- 随机服务系统:RSS(Random Service System)在服务时从等待顾客中随意抽取一个进行服务。
- 优先服务和动态优先服务:PR(Priority Service)预先规定优先顺序位的类别,且给到达顾客规定优先顺序位作为标记的优先权。通常按照FCFS服务,优先权分为三类:排队优先权、中断优先权、动态优先权。如计算机中断的优先级。
- 处理器共享:PS(Processor Sharing)服务台的处理能力被平均分配给队列中的所有顾客,没有排队现象出现,当顾客的数量增加时,只是顾客的服务时间边长。如:网络服务系统。
- 无限服务台:IS(Infinite Server)在这种情况下,队列中的每个顾客接收完全相同的服务,而且就好像它是唯一的一个顾客一样。好像对于每个顾客都可以“克隆”出一个心得服务台,而且克隆的数目可以无限。
- 服务时间分布:指数、常熟、k阶爱尔朗分布
3.排队规则
- 队列容量:有限/无限
- 排队方式:单队列、并联式多队列、串联式多队列、杂乱队列
4.数量指标
- 平均队长:排队系统中顾客数的平均值,
。
- 平均队列长:排队系统中等待服务的顾客数的平均值,
。
- 平均逗留时间:一个顾客在系统中停留的时间的平均值,
。
- 平均等待时间:一个顾客在系统中排队等待的时间的平均值,
。
- 稳态顾客数:
,表示当稳定时有
位顾客的概率。
- 平均到达率:单位时间内到达顾客的平均数
。
- 平均服务率:单位时间内被服务顾客的平均数
。
- 服务强度:单位时间内的服务强度,
。
二。常见的分布
1.泊松分布
- 需要满足的条件:
-
- 在
时间内,有一个顾客到达的概率为
。
- 没有一个顾客到达的概率
- 不可能多于一个顾客到达。
- 注意这里直接将
视为无穷小量
- 在
- 顾客到达服从参数为
的泊松流。
2.负指数分布
- 需要满足的条件:
-
- 在
时间内,有一个顾客被服务完的概率为
。
- 没有一个顾客被服务完的概率
- 不可能多于一个顾客被服务完。
- 注意这里直接将
视为无穷小量
- 在
- 服务时间服从参数为
。
三。排队模型记号
一般形式:X/Y/Z/A/B/X
-
- X顾客到达时间间隔分布。
- Y服务时间分布。
- Z服务台数目。
- A排队系统允许的最大顾客容量。
- B顾客总体数量。
- C排队规则(一般情况为先到先服务)。
四。单服务台模型
0.Little公式
运行指标之间的关系:
1.标准型M/M/1/ ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfin%2F%5Cinfin)
- 特点:
-
- 顾客源为无限的,顾客的到达相互独立,到达规律服从参数为
的泊松分布。
- 单服务台、队长无限、先到先服务。
- 各顾客的服务时间相互独立,且同服从于参数为
的负指数分布。
- 顾客源为无限的,顾客的到达相互独立,到达规律服从参数为
- 首先计算出来对应的P值:
- 计算出的参数结果:
2.系统容量有限型M/M/1/N/ ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfin)
损失制:当顾客到达时,所有的服务台均被占用,顾客随即离去。 首先计算出来对应的P值:
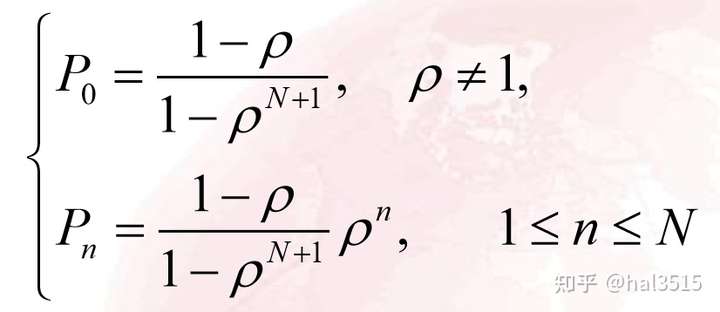
- 计算出的参数结果:
3.顾客源有限型M/M/1/ ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfin) /M
/M
首先说明一下,因为顾客源只有m,所以最多的情况就是来m个顾客,因此这个模型和 M/M/1/m/m 其实是完全一样的。 但是注意这里的 的定义和前面有一些区别,这里的
定义为单位时间内该顾客来到系统请求服务的次数。
- 下面首先计算出来对应的P值:
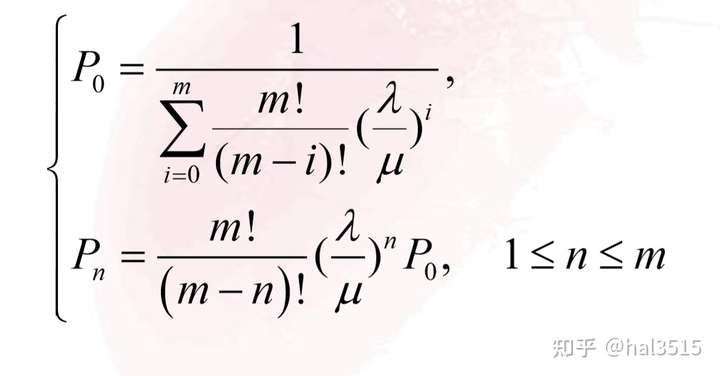
- 计算出的参数结果:
五。多服务台模型
1.多服务台标准型M/M/c/
- 顾客流为泊松流,平均到达率为
,各个服务台的平均服务率是
。
- 整个服务机构的平均服务率为
或
。
- 系统服务强度为(当
会产生排队现象)
- 首先计算出来对应的P值:
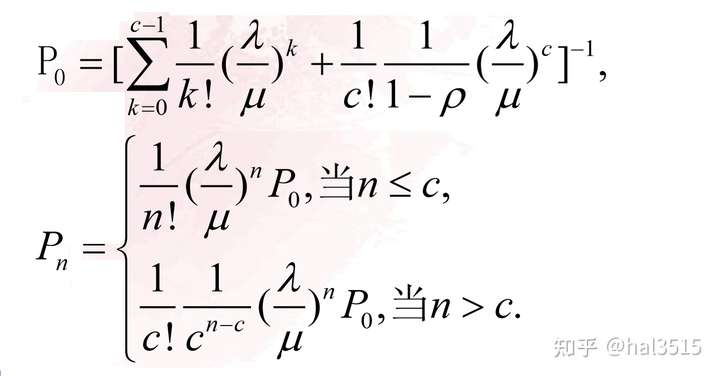
- 计算出系统的运行指标:
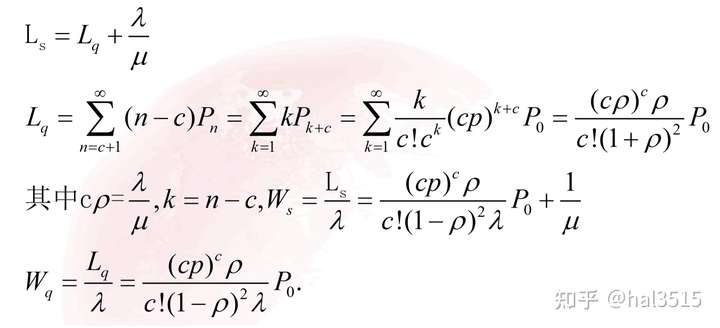
- 一个有用的结论: 顾客逗留时间服从
的指数分布(参考平均逗留时间
)。
2.多服务台M/M/c/N/ ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfin)
- 首先计算出来对应的P值:
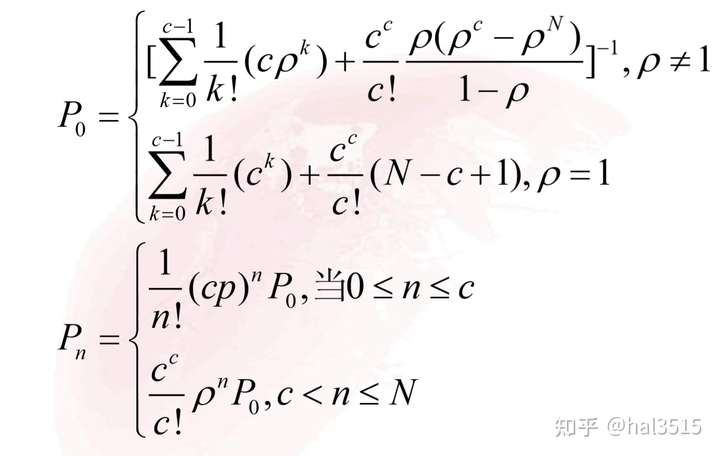
- 计算出系统的运行指标:
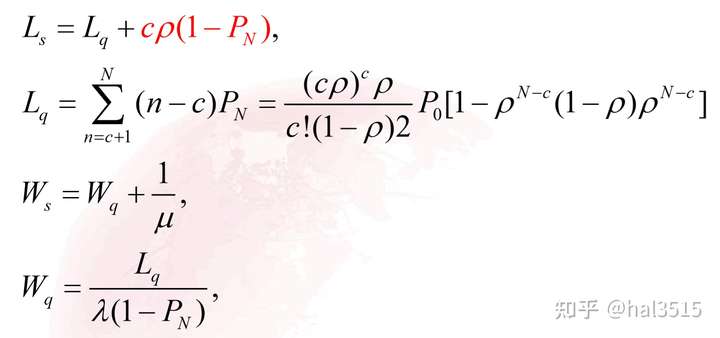
3.多服务台M/M/c/ ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfin) /m
/m
- 首先计算出来对应的P值:
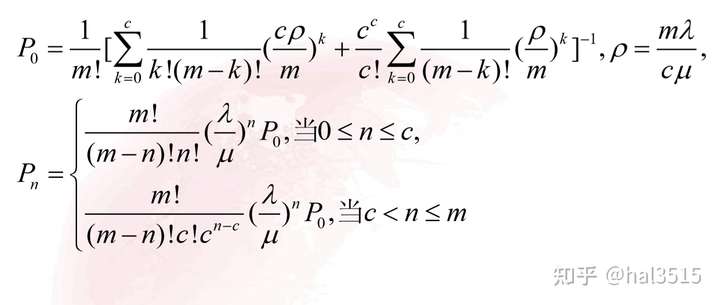
- 计算出系统的运行指标:
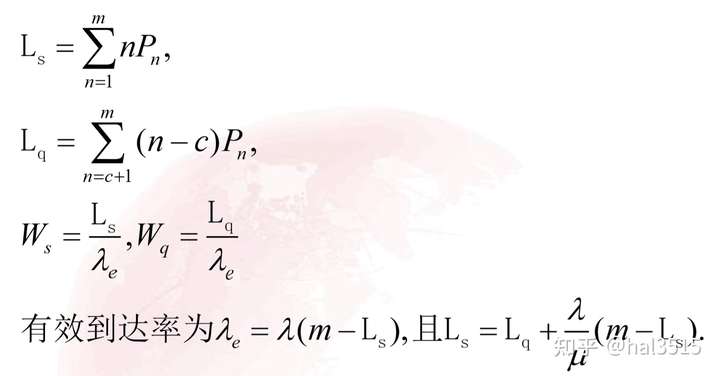
六。排队系统最优化
1.标准M/M/1系统的最优服务率
- 参数引入:
-
:对每个顾客的单位时间服务费。
:为每个顾客在系统停留单位时间的损失费。
:单位时间对每位顾客服务的收入。
:总费用。
- 优化目标(单位时间费用最小):
- 求得最优取值:
- 优化目标(服务利润最大):
(
表示排除没有人的情况)
2.系统容量有限M/M/1/N/ ![[公式]](https://www.zhihu.com/equation?tex=%5Cinfin) 的最优服务率
的最优服务率
- 与标准情况的差别:这里相当于如果系统中已经有
个顾客了,那么后来的都会被拒绝,所以说这里实际进入(稳定状态下服务完)的客户多一个
的系数,为
- 优化目标为:
- 求得结果:
注意这里面 ,其他的参量也都知道,因此最后只需要通过数值方法求解
。
3.顾客源有限M/M/1/m/m的最优服务率
- 根据之前的模型可知,单位时间服务完的顾客数为
。
- 优化目标(服务利润最大):
(
表示排除没有人的情况)
- 优化结果为:
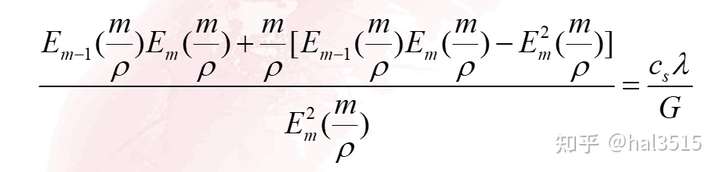
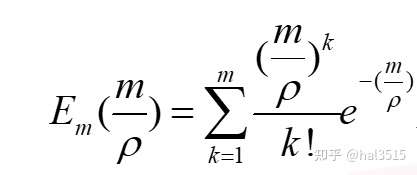
4.标准M/M/c的最优服务台数
- 优化目标(单位时间费用最小):
,注意这里因为
所以个服务台的个数有关。
- 由于
是离散的取值,因此采用边际分析法求解,假定
的最优值为
,此时
为最少费用。
- 根据最小值的特性可以得到如下的不等式:
- 化简得到结果:

本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 CJH's blog!






