图论

推荐博客

基本概念补充

图论中图是由点和边构成的，可以反映一些对象之间的关系。

无向图

无向图（简称图）：没有方向，由点和边构成的图，记做G =(V , E)，点是V，边是E。
注：图论的图与几何图、工程图不一样。

因为一般情况下的图中点的相对位置及点间连线长短，对于反映对象之间的关系并不是重要的。

联结$ v_{i1}$**和**$ v_{ik}$**的链**：在无向图G中，若存在一个点边的交错序列($ v_{i1}$,$ e_{i1}$,$ v_{i2}$,$ e_{i2}$,……$ v_{ik-1}$,$ e_{ik-1}$,$ c_{ik}$)其中$ v_{ik}$属于V(G),$ e_{ij}$属于E(G)。

联结 v_{i1} 和 v_{ik} 的圈：在上述的链中，若 v_{i1} = v_{ik}，也就是首尾相连。

连通图：对于一个无向图，若任何两个不同的点之间，至少存在一条链。

简单图：一个图如果它既没有环也没有平行边（两条边连接同一对顶点）,称为简单图(simple graph)。

完全图:其中每对不同的顶点之间都恰连有一条边相连

赋权图：对无向图的每一条边（$v_i$,$v_j$),都有一个数（称为权重）$w_ij$对应。

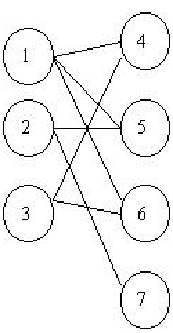
二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

顶点的度：与顶点v关联的边的个数称为顶点v 的
度(degree) （环计两度），记作 d(v) .

度为零的点称为弧立点，度为1的点称为悬挂点。悬挂点的关联边称为悬挂边。度为奇数的点称为奇点(odd point) ，度为偶数的点称为偶点(even point) 。

有向图

有向图：由点和弧构成的图，记做D =(V , A)，其中V是图D的点集，A是图D的弧集。
注：无向图是一种特殊的有向图，无向图的边实际上就是等 价于两条方向相反的弧。

联结$ v_{i1}$**和**$ v_{ik}$**的链**：在无向图G中，若存在一个点边的交错序列($ v_{i1}$,$ e_{i1}$,$ v_{i2}$,$ e_{i2}$,……$ v_{ik-1}$,$ e_{ik-1}$,$ c_{ik}$)其中$ v_{ik}$属于V(D),$ e_{ij}$属于V(D)。

联结 v_{i1} 和 v_{ik} 的回路：在上述的链中，若 v_{i1} = v_{ik}，也就是首尾相连。

赋权图：对无向图的每一条弧($v_i$ ,$v_j$ ),都有一个数（称为权重）$c_{ij}$对应。

网络：在赋权的有向图D中指定一点为发点(记为$v_s$)m指定另一点为收点（记为$v_t$),其余的点为中间点，并把 D 中的每一条弧的赋权数$c_i$, j称为弧($v_i$ ,$v_j$ )的容量，这样的赋权有向图 D 就称为网络。

图与网络的数据结构

描述图与网络的3种常用表示方法：邻接矩阵表示法、关联矩阵表示法、弧表表示法

邻接矩阵表示法

邻接矩阵表示法是将图以邻接矩阵（adjacency matrix）的形式存储在计算机中。图 G=(V,A) 的邻接矩阵是如下定义的：C是一个 n * n 的0-1矩阵

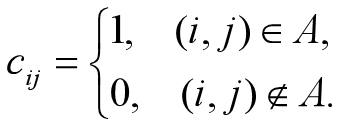
也就是说，如果两节点之间有一条弧，则邻接矩阵中对应的元素为1；否则为0。

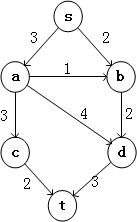
例一：对于下图，可以用邻接矩阵表示为

解释：现在有五个图，邻接矩阵a就是5 ∗ 5 5*55∗5的方阵，∵ 1→2，∴a[1][2]=1；∵1→3所以a[1][3]=1；∵ 4→3，∴a[4][3]=1，其他都是一样的，所有的都写出来就是：

同样，对于网络中的权，也可以用类似邻接矩阵的矩阵表示。只是此时一条弧所对应的元素不再是1，而是相应的权而已。如果网络中每条 弧赋有多种权，则可以用多个矩阵表示这些权。

关联矩阵表示法

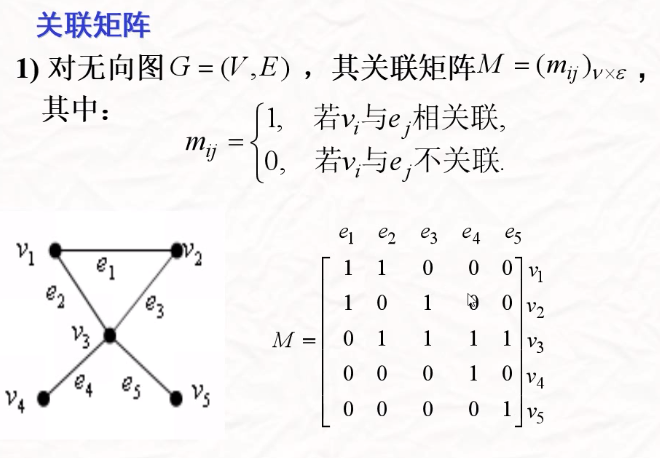
关联矩阵表示法是将图以关联矩阵（incidence matrix）的形式存储在计算机中．

$ \mathrm{B}=\left(\mathrm{b}{\mathrm{ik}}\right){\mathrm{n} * \mathrm{~m}} \in(-1,0,1)^{\mathrm{n} * \mathrm{~m}} $的关联矩阵B是如下定义，B是一个N*M的矩阵，即

如果一个顶点是一条弧的起点，则关联矩阵中对应的元素为1；如果一个顶点是一条弧的终点，则关联矩阵中对应的元素为-1；如果一个顶点与一条弧不关联，则关联矩阵中对应的元素为0。

例2 对于例1所示的图，如果关联矩阵中每列对应弧的顺序为 (1,2)，(1,3)，(2,4)，(3,2)，(4,3)，(4,5)，(5,3)和(5,4)，则关联矩阵表示为（列单位为弧）

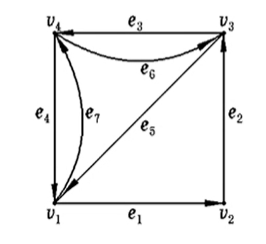
这个图有4个节点，7条连线，所以是4 ∗7的矩阵，每一列都是只有一个1，一个 -1。
看e1这条线，头是v1尾是v2，所以v1=1，v2=-1
e3，头是v3，尾是v4，所以v3是1，v4是-1；

弧表表示法

弧表表示法将图以弧表（arc list）的形式存储在计算机中。所谓图的弧表，也就是图的弧集合中的所有有序对。

假设例1中的弧(1,2)，(1,3)，(2,4)，(3,2)，(4,3)，(4,5)，(5,3)和(5,4)上的权分别为8，9，6，4，0，3，6和7，则弧表表示如下：

网络流模型

对于一个网络流我们可以用一个有向图G = （V，E，C）表示；V表示顶点的集合，E表示有向边的集合，C表示有向边的最大流量。对于每一个网络，有一个源输入点，称之为source，一个输出点，称之为sink。在不是出发点source也不是输出点sink的其他点，流量不能超过有向边的最大流量，这是一个约束条件。
下图就是一个简单的网络流模型：

https://blog.csdn.net/changyuanchn/article/details/17097807

最短路

最短路径问题
画图在线平台：
https://csacademy.com/app/graph_editor/
注意邻接矩阵和关联矩阵的概念！

邻接矩阵：元素为权值，不连接时为无穷(无权时为0/1表示是否相连)

解决方法：Dijkstra算法 Floyd算法
https://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
https://blog.csdn.net/weixin_43791406/article/details/89314614

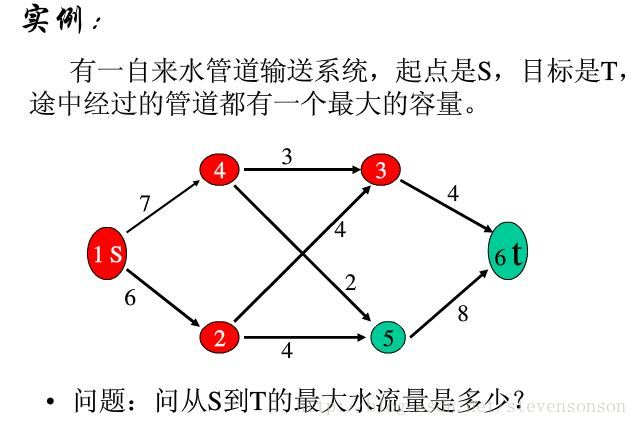
最大流

网络流图是一张只有一个源点和汇点的有向图，而最大流就是求源点到汇点间的最大水流量，下图的问题就是一个最基本，经典的最大流问题

流量,容量,可行流,增广路
https://blog.csdn.net/stevensonson/article/details/79177530

图就是一种管道，管道有最大通过流量的限制，图中边的权值就是所谓的“容量”。同时，注意有唯一的源点和汇点。
算法的关键在于
1）何为增广路径，如何找出增广路径。
2）如何更新流量
所谓增广路径，就是找到这样一条路径，其流量不满，未达到容量上限。
所有的可能的增广路径在一起便构成了残留网络
第一步，计算可增加流量
设某一增广路径上的节点为（a1,a2,a3,a4,…,an）
如果（u,v）是正向边，则增加流量d = min{ c(ai,aj) - f(ai,aj) | j = i +1, i =1,2,3…,n-1}
如果是逆向边，则增加流量d = min{ f(ai, aj) | j = i +1, i =1,2,3…,n-1}
第二步，更新流量
如果（u,v）是正向边，则 f(u,v) = f(u,v) + d
是逆向边，则f(u,v) = f(u,v) - d
注意，如果是逆向边，就是减法，当前管道从中减去部分流量，而且，伴随着这部分减去的流量，必有另一部分管道的流量会增加。。而且，最后的总流量增加了d
来自 https://www.cnblogs.com/ShaneZhang/p/3755479.html

最小生成树

图G=（V(G),E(G)）树T=（V(T),E’(T)）
在一个连通无向图G=(V, E)中，对于其中的每条边(u,v)∈E，赋予其权重w(u, v)，则最小生成树问题就是要在G中找到一个连通图G中所有顶点的无环子集T⊆E，使得这个子集中所有边的权重之和最小。
即生成树为一条连接所有点的路径，最小生成树为权重和最小那个生成树（非环）
解决最小生成树问题有两个算法：Prim算法和Kruskal算法
Prim算法基本思想是从选点开始，再选择和不连通点之间的边，进而循环，每一次循环中，一个关键在于判断点之间是否不连通（对连通点集团进行编号，即只需判断集团编号是否相等即可），另一个在于选择最小的边。
Kruskal算法基本思想是从选最小边开始，连通成一个集团，进行编号，再选择不连通的集团的最小赋权边进行连接，依次循环。

https://blog.csdn.net/luoshixian099/article/details/51908175